통계 용어
abridged life table 간이생명표
absolute deviation 절대편차
absolute error 절대오차
absolute frequency 절대도수[빈도]
absolute moment 절대적률
absolute rank 절대순위
absolutely continuous 절대연속(의)
absolutely continuous distribution 절대연속분포
absolutely integrable 절대적분가능(한)
absorbing barrier 흡수벽, 흡수장벽
absorbing distribution 흡수분포
absorbing region 흡수역
absorbing state 흡수상태
accelerated life test 가속(적)수명시험
accelerated stochastic approximation 가속(적)확률근사
accelerating stress 가속 스트레스
acceleration function 가속함수
accept 채택하다, 수용하다
acceptable boundary 합격경계, 수용경계
acceptable quality level 합격품질수준
acceptable reliability level 합격신뢰도수준
acceptance control chart 합격관리도
acceptance criterion 합격기준
acceptance error 합격오류, 채택오류
acceptance inspection 합격검사
acceptance line 합격선
acceptance number 합격수, 합격판정개수
acceptance region 채택역, 수용역
acceptance sampling by attributes 계수형 합격 샘플링
acceptance sampling by variables 계량형 합격 샘플링
acceptance sampling 합격 샘플링, 합격판정 샘플링
accessible 도달가능(한)
accessible state 도달가능상태
accumulated process 누적과정, 집적과정
accumulated sum 누계, 누적합, 쌓인 합
accumulation analysis 누적분포
accuracy 정확도
action space 행동공간, 행위공간
actuarial mathematics 보험수학
actuarial statistics 보험통계(학)
adaptive 적응적
adaptive estimator 적응추정량, 순응추정량
adaptive inference 적응추론, 순응추론
adaptive method 적응법, 순응법
adaptive optimization 적응최적화, 순응최적화
adaptive test 적응검정[검증]
added variable plot 추가변수그림, 추가변수도
addition law of probability 확률의 덧셈법칙
addition theorem 덧셈정리, 가법정리
additional sample 추가표본
additive 가법(적), 더하기
additive effect 가법효과, 더하기 효과
additive model 가법모형, 더하기 모형
additive process 가법과정
additive property 가법성질
additive risk model 가법위험모형
additivity 가법성
adjacent category 이웃범주
adjacent matrix 이웃행렬
adjacent value 인접값
adjoint matrix 수반행렬, 딸림행렬
adjusted coefficient of determination 수정결정계수
adjustment factor 수정[보정]인자
admissibility 허용가능성, 허용성
admissible 허용가능, 허용
admissible estimator 허용가능추정량, 허용추정량
admissible number 허용가능수, 허용수
admissible strategy 허용가능전략, 허용전략
admissible test 허용가능검정[검증], 허용검정[검증]
affinity 유사성
affinity-alpha resolvability 유사알파 분해성
affinity transformation 유사성변환
age composition 나이구성, 연령구성
age dependent 나이의존, 연령의존
age-specific death rate 나이별 사망률 , 연령별 사망률
agglomerative algorithm 응집알고리즘
aggregate 총
aggregation 총계
aggregation bias 총계편향
aggregative index 총계지수
aggregative method 총계법
agricultural census 농업총조사, 농업센서스
agricultural trial 농업시험
Aitken's estimator 에이트켄의 추정량
Akaike's information criterion 아캉케의 정보(량)기준
algebra 대수(학)
algorithm 알고리즘, 계산절차
alias 별명
allocation 배분, 할당
allometry 이질동형
allowable defects 허용결점수
all possible regression 모든 가능한 회귀, 총가능회귀
almost all 거의 모든
almost certain 거의 확실한
almost certainly 거의 확실하게
almost everywhere 거의 모든 곳에서
almost stationary 거의 정상적인
almost sure 거의 확실한
almost sure convergence 거의 확실한 수렴
almost surely 거의 확실하게
almost surely stable 거의 확실하게 안정된
alpha-resolvability 알파 분해성
alternating least squares 교대최소제곱
alternating matrix 교대행렬
alternating renewal process 교대갱신과정
alternating series 교대급수
alternative form method 동형방법
alternative hypothesis 대립가설, 대안가설
amalgamated sum 융합합
amount of information 정보량
amount of inspection 검사량
amplitude 진폭
amplitude ratio 진폭비
analogue computer 아날로그 컴퓨터
analysis 분석, 해석, 해석학
analysis of covariance 공분산분석
analysis of deviance 이탈도[편차]분석
analysis of dispersion 산포분석, 퍼짐분석
analysis of variance [ANOVA] 분산분석
analysis of variance [ANOVA] table 분산분석표
analysis survey 분석조사
analytic function 해석(적)함수
analytic trend 해석적 추세
ancillary information 보조정보
ancillary statistic 보조통계량
Anderson-Darling statistic 앤더슨-달링 통계량
Andrews plot 앤드류스 그림
angle of reflection 반사각
angular transformation 각변환
angular variation 각변동
annealing 담금질
annihilator space 소멸자 공간
annual rate of growth 연간성장률
Anosov's theorem 아노소프의 정리
Ansary-Bradley statistic 안사리-브래들리 통계량
antimode 반최빈값
antirank 반순위
antisymmetric 반대칭(적)
antithetic variate 대조변량
antitonic function 순서역전함수
aperiodic 비주기적
aperiodic state 비주기적상태
apparent failure rate 겉보기 고장률, 외견고장률
apparent rate 겉보기 비율
applied mathematics 응용수학
applied statistics 응용통계학
approximate distribution 근사분포
approximate integration 근사적분
approximate solution 근사해
approximate value 근사값
approximation 근사, 어림셈
approximation error 근사오차
approximation method 근사방법
approximation theorem 근사정리
arbitrary 임의의
arccosine 아크코사인, 역코사인
arcsecant 아크시컨트, 역시컨트
arcsine 아크사인, 역사인
arcsine distribution 아크사인분포, 역사인분포
arctangent 아크탄젠트, 역탄젠트
area 넓이, 면적
area comparability factor 지역비교인자
area sampling 지역표집, 지역추출법
area statistics 지역통계
area under the curve 곡선아래면적, 곡선밑면적
argument 변수, 편각
arithmetic 산술, 셈법, 산수
arithmetic average 산술평균
arithmetic distribution 산술분포
arithmetic mean 산술평균
arithmetic sequence 등차수열
arithmetic series 등차급수
Armitage's restricted procedure 아미타지의 제한절차
array 배열
arrival distribution 도착분포
arrow diagram 화살그림, 화살도
artificial intelligence 인공지능
ascertainment error 확인오차
assay 시험, 생검
assembly language 어셈블리어(語)
assignable cause 이상원인
assignable variation 이상변동
associable design 동반설계
associate class 동반층, 동반류
association 연관성
association analysis 연관성분석
association scheme 동반계획
associative law 결합법칙, 묶음법칙
assortative mating 동류교배
assumption 가정
asymmetric distribution 비대칭분포
asymmetric relation 비대칭관계
asymmetrical test 비대칭검정[검증]
asymmetry 비대칭성
asymptote 점근선
asymptotic 점근적(인)
asymptotic Bayes procedure 점근적 베이즈 절차
asymptotic bias 점근편향
asymptotic distribution 점근분포
asymptotic efficiency 점근효율
asymptotic expansion 점근적 전개
asymptotic normality 점근적 정규성
asymptotic property 점근적 성질
asymptotic relative efficiency 점근적 상대효율
asymptotic series 점근급수
asymptotic standard error 점근(적)표준오차
asymptotic variance 점근분산
asymptotically efficient estimator 점근적 유효추정량
asymptotically locally optimal design 점근적 국소최적설계
asymptotically most powerful 점근적 최강력
asymptoticaly stationary 점근적 정상
asymptoticaly unbiased 점근적 비편향
atom of probability measure 확률측도의 원자
at random 임의로, 랜덤하게, 확률적으로
attack rate 발병률
attributable risk 귀속위험
attribute 속성
augmentation 확대, 덧붙임
augmented factorial experiment 확대요인실험, 덧붙인 요인실험
augmented matrix 확대행렬, 덧붙임(덧붙인)행렬
augmented posterior 확대사후분포
autocorrelation 자기상관
autocorrelation coefficient 자기상관계수
autocorrelation function 자기상관함수
autocovariance 자기공분산
autocovariance function 자기공분산함수
autocovariance generating function 자기공분산생성함수
automatic classification 자동분류
automatic process control 자동공정관리
autoregression 자기회귀
autoregressive integrated moving-average [ARIMA] 자귀회귀누적이동평균
autoregressive moving-average [ARMA] 자기회귀이동평균
autoregressive process 자기회귀과정
autoregressive transformation 자귀회귀변환
autospectrum 자기 스펙트럼
availability 가용도
average 평균
average amount of inspection 평균검사량
average deviation 평균편차
average error 평균오차
average extra defectives limit 평균여분불량수한계
average fraction inspection [AFI] 평균검사비율
average linkage 평균연결(법)
average method 평균법
average number of defects 평균결점수
average outgoing quality 평균출검품질
average outgoing quality level 평균출검품질수준
average outgoing quality limit 평균출검품질한계
average quality 평균품질
average quality protection 평균품질보호
average run length 평균 런 길이
average sample 평균표본
average sample number 평균표본수
average sample number curve 평균표본수곡선
average sample number function 평균표본수함수
average total inspection 평균총검사량
average value 평균값
axial point 축점
axiom 공리
axiom of choice 선택의 공리
axiom of probability 확률의 공리
axiomatic method 공리적 방법
axis 축
axis of abscissas 가로축, 횡축
axis of coordinates 좌표축
axis of ordinates 세로축, 종축
axis of rotation 회전축
axis of symmetry 대칭축
back forecasting 후방예측
back substitution 후방대입
background factor 배경요인, 배경인자
backward difference 후진차분
backward diffusion equation 후진확산방정식
backward elimination 후진제거, 변수제거
backward elimination method 후진제거법, 변수제거법
backward equation 후진방정식
backward induction 후진귀납법
backward martingale 후진 마팅게일
backward operator 후진연산자
Bahadur efficiency 바하두르 효율
Bahadur relative efficiency 바하두루 상대효율
balance 균형
balanced array 균형배열
balanced confounding 균형중첩, 균형혼선
balanced data 균형자료
balanced factorial design 균형요인설계
balanced incomplete block design [BIBD] 균형불완비블록설계
balanced sample 균형표본
ballot 투표
ballot theory 투표이론
Banach space 바나흐 공간
band 띠, 대역
band chart 띠그림표, 띠도표
band graph 띠그래프
bandwidth 띠너비, 띠폭, 대역폭
bar chart 막대그림표, 막대도표
Bartholomew's problem 바솔로뮤의 문제
Bartlett correction 바틀렛 수정
Bartlett estimator 바틀렛 추정량
base 기저, 기준, 밑변, 밑, 바탕, 밑면
base curve 기저곡선, 밑곡석
base line 기준선, 밑선, 밑금
base year 기준년(도)
basic form 기본꼴, 기본형
basis 기저, 밑 , 바탕
Basu's theorem 바수의 정리
batch 뱃치, 집단, 묶음
Bates-Neyman model 베이츠-네이만 모형
bath tub curve 욕조(형)곡선
Bayes estimate 베이즈 추정값
Bayes formula 베이즈 공식
Bayes procedure 베이즈 절차
Bayes rule 베이즈 규칙
Bayes theorem 베이즈 정리
Bayesian inference 베이즈(적)추록
Bayesian information criterion 베이즈 정보기준
Bayesian interval 베이즈 구간
Bayesian method 베이즈 방법
bead experiment 구슬실험
Behrens-Fisher test 베렌스-피셔 검정[검증]
Bellman-Harris process 벨만-해리스 과정
bell-shaped curve 종형곡선
bell-shaped distribution 종형분포
Beran's test 베란의 검정[검증]
Berge's inequality 버지의 부등식
Berkson model 버크슨 모형
Bernoulli distribution 베르누이 분포
Bernoulli number 베르누이 수
Bernoulli polynomial 베르누이 다항식
Bernoulli trial 베르누이 시행
Bernoulli variation 베르누이 변동
Bernoulli's inequality 베르누이의 부등식
Bernstein's inequality 번스타인의 부등식
Bernstein's theorem 번스타인의 정리
Bessel equation 베셀 방정식
Bessel function 베셀 함수
Bessel interpolation 베셀 보간법
best asymptotic normal [BAN] 최량점근정규
best critical region 최량임계역, 최량기각역
best fit 최량적합
best invariant decision function 최량불변결정함수
best linear estimator 최량선형추정량
best linear index 최량선형지수
best linear unbiased estimator 최량선형비편향추정량
best subset regression 최량부분집합회귀
best test 최량검정[검증]
best unbiased critical region 최량비편향임계[기각]역
beta-binomial distribution 베타-이항 분포
beta distribution 베타 분포
beta-Stacy distribution 베타-스테이시 분포
beta-Whittle distribution 베타-위틀분포
between class 계급간
between class variation 계급간 변동
between cluster variance 군집간 분산, 집락간 분산
between group 그룹간
between groups variance 그룹간 분산
Bhattacharyya bound 바타차리야 한계
Bhattacharyya's distance 바타차리야의 거리
bias 편향, 치우침, 편의(偏倚)
bias parameter 편향모수
bias reduction 편향축소, 치우침 줄이기
biased 편향(된), 치우친
biased coin 편향동전
biased estimation 편향추정
biased regression 편향회귀
biased sample 편향표본
biased test 편향검정[검증]
Bickel-Hodges estimator 빅켈-핫지스 추정량
bicubic spline 쌍삼차 스프라인, 겹삼차 스플라인
Bienayme-Tchebychev inequality 비에나메-체비셰프 부등식
bifactor model 이인자모형
bijection 전단사함수, 전단사
bijective 전단사의, 전단사
bijective function 전단사함수, 일대일 대응함수
bijective mapping 전단사사상, 일대일 대응사상
bilinear form 겹선형형식
bilinear function 겹선형함수
bilinear model 겹선형모형
bilinear transformation 겹선형변환
bimodal distribution 이봉분포
binary comparisons 이진비교
binary data 이진수자료
binary expansion 이진전개
binary number 이진수
binary number system 이진수체계
binary operation 이항연산
binary relation 이항관계
binary response 이항반응
binary search 이분탐색
binary sequence 이진수열
binary system 이진법
Bingham's distribution 빙햄의 분포
binomial 이항(의)
binomial coefficient 이항계수
binomial distribution 이항분포
binomial equation 이항방정식
binomial expansion 이항전개
binomial formula 이항공식
binomial index of dispersion 이항산포지수
binomial probability paper 이항확률지
binomial proportion 이항비율
binomial random variable 이항확률변수
binomial series 이항급수
binomial test 이항검정[검증]
binomial theorem 이항정리
binomial variation 이항변도
bioassay 생시험
bioavailability 생가용도, 생물적 가용도
bioequivalence 생동등성
biological assay 생물학적 시험
biological indicator 생물학적 지표
biometrics 계량생물학
biometry 생물측정
biostatistics 생물통계학
biplot 행렬도, 쌍도
bipolar factor 양극인자, 쌍극인자
Birnbaum's inequality 번바움의 부등식
Birnbaum-Saunders distribution 번바움-손더스 분포
Birnbaum-Tingey distribution 번바움-틴지 분포
birth-and-death process 출생-사망 과정, 생성-소멸 과정
birth-death ratio 출생(대)사망 비
birth process 출생과정
birth rate 출생률
birthday problem 생일문제
birthplace population 출생지인구
bisection method 이분법
biserial correlation 이연상관
biserial correlation coefficient 이연상관계수
bispectrum 이변량 스펙트럼, 쌍 스펙트럼
Bissinger distribution 비싱거 분포
bit 비트
bivariate 이[2]변량
Blackwell's theorem 블랙웰의 정리
blind trial 눈가림시행
block 블록
block effect 블록 효과
block product 블록 곱
Bochner's theorem 보크너의 정리
body graph 신체 그래프
Bonferroni inequality 본페로니 부등식
Boole's inequality 부울의 부등식
Boole-Bonferroni-Frechet inequality 부울-본페로니-프레셰 부등식
boolean algebra 부울 대수
Boolean model 부울 모형
Boolean ring 부울 환
bootstrap 붓스트랩, 자육(自育)
Borel-Cantelli lemma 보렐-칸텔리 보조정리
Borel field 보렐 집합체, 보렐 체
Borel measurability 보렐 가측성
Borel measurable function 보렐 가측함수
Borel measure 보렐 측도
Borel set 보렐 집합
Borel-Tanner distribution 보렐-태너 분포
Borges' approximation 보르그즈의 근사
Bose-Einstein statistic 보즈-아인슈타인 통계량
boundary 경계
boundary condition 경계조건
boundary value 경계값
boundary value problem 경계값문제
bounded 유계
bounded above 위로 유계
bounded below 아래로 유계
bounded completeness 유계완비성
bounded convergence 유계수렴
bounded convergence theorem 유계수렴정리
bounded function 유계함수
bounded linear functional 유계선형범함수
bounded set 유계집합
bounded variation 유계변동
box-and-whisker plot 상자수염도, 상자그림
Box-Cox transform 박스-칵스 변환
Box-Jenkins model 박스-젠킨스 모형
Box-Muller transformation 박스-뮬러 변환
box plot 상자그림
bracket 큰 묶음표, 대괄호
Bradley-Terry model 브래들리-테리 모형
branch 분지, 가지
branching process 분지과정, 분기과정
break point 단락점
breakdown bound 붕괴한계, 붕괴경계
breakdown point 붕괴점
breeding 육종
Brendt-Snedecor method 브렌트-스네데카 방법
Brown-Mood procedure 브라운-무드 절차
Brownian bridge 브라운 다리
Brownian motion 브라운 운도
brownian motion with drift 표류(하는)브라운 운동
Brunk's test 프렁크의 검정[검증]
bubble sort 거품순서화
Buffon's needle problem 뷔퐁의 바늘문제
bulk sampling 덩어리 표집
Burke's theorem 버크의 정리
Burkholder approximation 버크홀더 근사
Burt matrix 버크 행렬
business census 사업체총조사
business composite index 경기종합지수
business diffusion index 경기확산지수, 경기동향지수
business index 경기지수
business survey index 기업실사지수
calculation 계산, 셈
calibration 보정, 눈금조정
call-back 재조사
canonical 정준(적), 표준(적)
canonical basis 정준기저, 표준기저
canonical correlation 정준상관, 표준상관
canonical correlation analysis 정준상관분석, 표준상관분석
canonical correlation coefficient 정준상관계수, 표준상관계수
canonical discriminant analysis 정준판별분석, 표준판별분석
canonical form 정준형, 표준형, 표준꼴
canonical ling 정준연결(함수), 표준연결
canonical score 정준점수, 표준점수
canonical structure 정준구조, 표준구조
canonical variate 정준변량, 표준변량
Cantelli's inequality 칸텔리의 부등식
Cantor-type distribution 칸토르형 분포
capture-recapture sampling 포획-재포획 표집
cardinal number 기수, 집합의 크기
carrier epidemic model 매개체전염모형
carrier variable 운반변수
carry-over effect 이월효과
Cartesian product 데카르트 곱
case-control study 사례-대조 연구
case history study 사례사연구
Castle's law 캐슬의 법칙
categorical data 범주형자료
categorical distribution 범주형분포
categorical variable 범주형 변수
categorization 범주화
category 번주
category attribute 범주속성
Cauchy distribution 코쉬 분포
Cauchy-Schwarz inequality 코쉬-슈바르츠 부등식
cause 원인
cause-and-effect diagram 인과도, 특성요인도
cause of death 사인, 사망원인
cell 칸
cell frequency 칸도수[빈도]
censored data 중도절단자료, 중절자료
censored regression 중도절단회귀, 중절회귀
censored sample 중도절단표본, 중절표본
censoring 중도절단, 중절
census 총조사, 센서스, 전수조사
census of housing 주택총조사
census of population 인구총조사
census tract 총조사 조사구, 센서스 조사구
center 중심, 중앙
centering 중심화
central composite design 중심합성설계
central factorial moments 중심계승적률
central limit theorem 중심극한정리
central moment 중심적률
central tendency 중심경향성, 중심성향
central value 중심값
centroid 무게중심, 중심(重心)
chain 연쇄, 사슬
chain-binomial model 연쇄이항모형
chain block design 연쇄 블록 설계
chain rule 연쇄법칙
Champernowne distribution 챔퍼나운 분포
chance 우연
chance cause 우연원인
chance variation 우연변동
change of variables 변수바꿈, 변수변환
change-over design 전환설계
change-over trial 전환시행
change point 변화시점, 변화점
Chapman-Kolmogorov equation 채프만-콜모고로프 방정식
character 문자
characteristic curve 특성곡선
characteristic equation 특성방정식, 고유방정식
characteristic function 특성함수, 고유함수
characteristic root 특성근, 고유근
characteristics 특성
Chariler distribution 샤리에 분포
Chariler polynomial 샤리에 다항식
chart 도표, 그림표, 관리도
Chauvenet's criterion 쇼브네트의 기준
Chebyshev inequality 체비셰프 부등식
check sheet 점검지, 체크시트
Chernoff face 체르노프 얼굴
chi-function 카이 함수
chi-square 카이제곱
chi-squre distribution 카이제곱분포
chi-squre random variable 카이제곱확률변수
chi-square statistic 카이제곱통계량
chi-square test 카이제곱검정[검증]
chip experiment 칩 실험
Cholesky decomposition 콜레스키 분해
chunk sampling 덩어리 표집
circular chart 원도표, 원그림
circular distribution 원형분포
circular formula 순환식
circular normal distribution 원형정규분포
circula permutation 원형순열
circular quartile deviation 원형사분편차
circular range 원형범위
circular triad 원형삼각관계
class 계급
class boundary 계급경계
class frequency 계급도수[빈도]
class interval 계급구간
class lower limit 계급하단, 계급하한
class smbol 계급기호
class upper limit 계급상단, 계급상한
class value 계급값
class width 계급폭
classification 분류
classification statistic 분류통계량
climbing method 등산법
clinical epidemiology 임상역학
clinical trial 임상시험, 임상시행
closed 닫힌
closed-ended question 폐쇄형질문
closed form 닫힌 형식, 폐쇄형
closed formula 닫힌 공식
closed interval 닫힌 구간, 폐구간
closed sequential sampling 닫힌 순차적 표집, 폐순차적 표집
closed sequential test 닫힌[폐]순차적 검정[검증]
closed set 닫힌 집합, 폐집합
cluster 군집, 집락
cluster analysis 군집분석, 집락분석
cluster sampling 군집표집, 집락표집
cluster size 군집크기, 집락크기
Cochran's criterion 코크란의 기준
Cochran's test 코크란의 검정[검증]
Cochran's theorem 코크란의 정리
Cochran-Armitage test 코크란-아미티지 검정[검증]
Cochrane-Orcutt iterative process 코크레인-어컷트 반복절차
code 코트, 부호
coding 코딩, 부호화
coefficient 계수
coefficient of confidence 신뢰계수
coefficient of detrmintion 결정계수
coefficient of elasticity 탄력성계수
coefficient of reliability 신뢰성계수, 신뢰성
coefficient of variation [CV] 변동계수, 변이계수
cofactor 여인수
cograduation 동순위
Cohen's measure of agreement 코헨의 합치도
coherence 일관성
coherent structure 응집구조
cohort analysis 코호트 분석
cohort study 코호트 연구
collapsed stratum method 붕괴층방법
collapsibility 붕괴가능성
collection 모임, 집합
collinearity 공선성, 공선형성
column 열
column vector 열 벡터
combination 조합
combiantion of tests 검정[검증](의) 결합
combinatorial arrangement 조합배열
combiantorial test 조합검정[검증]
combinatorics 조합이론
combined estimator 결합추정량
common factor 공통인자
common factor variance 공통인자분산
communality 공통성
communicating 상호도달가능(한)
communicating class 상호도달가능집단
commutative law 교환법칙
comparative assay 비교시험
comparative mortality figure 비교사망자수
comparative mortality index 비교사망지수
compensating error 보상오차
competing risk model 경쟁위험모형
complement 여집합, 보집합, 나머지 집합
complementary 여, 보
complementary event 여사건, 보사건, 나머지 사건
complementary log-log 보 로그-로그
complete 완비, 완전
complete block 완비 블록
complete class 완비류
complete confounding 완전중첩, 완전혼선
complete enumeration 전부조사
complete life table 완전생명표
complete linkage 최장연결(법), 완전연결(법)
complete measure 완비측도
complete metric space 완비거리공간
complete space 완비공간
complete sufficient statistic 완비충분통계량
completely balanced 완전균형
completely randomized design 완전임의화설계, 완전확률화설계
completeness 완비성
complex Gaussian distribution 복소 가우스 분포
complex-valued function 복소값함수
complex variable 복소변수
complex Wishart distribution 복소 위샤트 분포
component 성분, 부품
component bar chart 성분막대도표
composite design 복합설계, 합성설계
composite hypothesis 복합가설
composite index 종합지수, 복합지수
composite sampling scheme 복합표집설계
composite system 복합시스템
composition of population 인구구성
compound event 복합사건
compound experiment 복합실험
compound frequency distribution 복합도수[빈도]분포
compound hypergeometric distribution 복합초기하분포
compound Poisson distribution 복합 포아송 분포
compound Poisson process 복합 포아송 과정
compressed limit 압축한계
computation 계산, 셈
concave 오목
concavity 오목성
concentration coefficient 집중계수
conceptual population 개념(적)모집단
conclusion 결론
concomitance 병존, 병재
concordance 부합성, 일치성
concordant 부합하는, 일치하는
concurrent deviation 병행편차
condition 조건, 상태
condition number 상태수, 조건수
conditional 조건부(의)
conditional convergence 조건부수렴
conditional density 조건부밀도
conditional density function 조건부 밀도함수
conditional distribution 조건부분포
conditional expectation 조건부기대
conditional failure rate 조건부고장률
conditional independence 조건부독립(성)
conditional inference 조건부추론
conditional likelihood 조건부가능도
conditional mean 조건부평균
conditional probability 조건부확률
conditional survival function 조건부생존함수
conditional test 조건부검정[검증]
conditionally complete 조건부완비
conditionally unbiased 조건부비편향
confidence band 신뢰대(역), 신뢰띠
confidence coefficient 신뢰계수
confidence curve 신뢰곡선
confidence interval 신뢰구간
confidence level 신뢰수준
confidence limit 신뢰한계
confidence region 신뢰영역
confidence set 신뢰집합
configuration 형태
confirmatory data analysis 확증적 자료분석
confluence analysis 합류분석
confounding 중첩, 혼선, 혼재, 교락
confounding bias 중첩편향, 혼선편향
confounding factor 중첩요인
confounding method 중첩법
confounding variable 중첩변수
confusion rate 혼동
congruential method 합동법
conjoint analysis 컨조인트 분석
conjugate 켤레, 공액
conjugate class 켤레류, 공액류
conjugate direction search method 켤레방향탐색법
conjugate distribution 켤레분포, 공액분포
conjugate gradient method 켤레경사도법
conjugate prior distribution 켤레사전분포, 공액사전분포
conjugate space 켤레공간, 공액공간
connectedness 연결성
consecutive test 계속적 검정[검증]
conservative test 보수적 검정[검증]
consistency 일치성
consistent 일치(적)
consistent equation 해를 갖는 방정식
consistent estimator 일치추정량
consistent statistic 일치통계량
consistent system 해를 갖는 방정식계
consistent test 일치검정[검증]
constant 상수
constant term 상수항
constraint 제약(조건)
construct 구인(構因)
construct validity 구인타당성
consumer price index 소비자물가지수
consumer price survey [CPS] 소비자물가조사
consumer's risk 소비자위험
consumption function 소비함수
contagious distribution 감염분포, 오염분포
contaminated distribution 오염분포
contaminated normal distribution 오염정규분포
contaminated variable 오염변수
contamination model 오염모형
content analysis 내용분석
content validity 내용타당성
contingency 우발성
contingency coefficient 우발성계수
contingency table 분할표, 우발표
continuity 연속성
continuity correction 연속성수정
continuous 연속적, 연속(의)
continuous data 연속자료, 연속데이터
continuous distribution 연속분포
continuous mapping 연속사상
continuous measure 연속측도
continuous population 연속모집단
continuous probability distribution 연속확률분포
continuous probability law 연속확률법칙
continuous process 연속과정
continuous random variable 연속확률변수
continuous sample space 연속표본공간
continuous sampling plan 연속표집계획
continuous time Markov chain 연속시간 마르코프 연쇄
continuous variable 연속변수
continuous variate 연속변량
continuously differentiable 연속미분가능
contour(line) 등고선
contour level 등고수준
contradict 모순이다
contradiction 모순
contraposition 대우
contrast 대비
contribution ratio 기여비
control 대조, 관리, 제어
control chart 관리도
control chart for attributes 계수형 관리도
control chart for variables 계량형 관리도
control group 대조군, 대조 그룹
control inspection 관리검사
control level 관리수준
control limit 관리한계
control of substrata 부층관리
control sheet 관리지
control treatment 대조처리
control variable 제어변수
controlled experiment 제어실험
converge 수렴한다
convergence 수렴
convergence in distribution 분포수렴
convergence in measure 측도수렴
convergence in probability 확률수렴
conversion 전환
convex 볼록(한)
convex function 볼록함수
convex hull 최소볼록집합
convex set 볼록집합
convolution 합성곱, 포갬
convolution formula 합성곱공식
Cook's distance 쿡의 거리
coordinate 좌표
coordinate axis 좌표축
coordinate plane 좌표평면
coordinate system 좌표계
coordinate transformation 좌표변환
Cornish-Fisher expansion 코니쉬-피셔 전개
corollary 따름정리
corrected moment 수정적률
correction 수정
correction for continuity 연속성수정
correction for grouping 그룹화수정
correlation 상관
correlation coefficient 상관계수
correlation coefficient matrix 상관계수행렬
correlation diagram 상관도
correlation function 상관함수
correlation matrix 상관행렬
correlation ratio 상관비
correlation table 상관표
correlogram 상관도표
correspondence analysis 대응분석
cospectrum 공(共)스펙트럼
cost function 비용함수
cost of living 생계비
countability axiom 가산공리
countable 가산의, 셀 수 있는
countable probability space 가산확률공간
countable set 가산집합, 셀 수 있는 집합
counter example 반례
counting measure 셈측도, 계수측도
counting process 셈과정, 계수과정
covariance 공분산
covariance function 공분산함수
covariance matrix 공분산행렬
covariance structure model 공분산구조모형
covariate 공변량
covariation 공변동
covariogram 공변동도
coverage 포함
coverage accuracy 포함정확도
coverage error 포함오차
coverage probability 포함확률
Craig's theorem 크레이그의 정리
Cramer's rule 크래머의 규칙
Cramer-Rao inequality 크래머-라오 부등식
cramer-von Miss test 크래머-폰미제스 검정[검증]
credible interval 신뢰구간, 신용구간
criterion 기준
criterion for stratification 층화기준
criterion-related validity 기준관련 타당성
critical condition 임계조건, 기각조건
critical failure 결정적 고장, 임계고장
critical level of significance 임계유의수준, 기각유의수준
critical point 임계점, 기각점
critical region 임계역, 기각역
critical value 임계값, 기각값
Cronbach's alpha 크론바흐의 알파
cross amplitude spectrum 교차진폭 스펙트럼
cross classification 교차분류
cross correlation 교차상관
cross covariance 교차공분산
cross-over design 교차설계
cross product 교차곱, 벡터곱, 외적
cross-product ratio 교차곱의 비
cross range 교차범위
cross-sectional analysis 횡단면분석
cross-sectional study 횡단면연구
cross spectrum 교차 스펙트럼
cross tabulation 교차표, 교차제표
cross-validation 교차타당성(입증)
crossed factor 교차요인
crude birth rate 조(粗)출생률
crude death rate 조(粗)사망률
crude moment 조(粗)적률
cubic lattice 입방격자
cubic spline 삼차 스플라인
cuboidal lattice design 입방형격자설계
cumulant 누율 누적적률
cumulant generating function 누율, 생성함수
cumulative distribution function 누적분포함수
cumulative error 누적오차
cumulative failure curve 누적고장곡선
cumulative frequency 누적도수[빈도]
cumulative frequency distribution 누적도수[빈도]분포
cumulative hazard function 누적위험함수
cumulative hazard rate 누적위험률
cumulative incidence 누적발생률
cumulative logit 누적 로짓
cumulative process 누적과정
cumulative relative frequency 누적상대도수[빈도]
cumulative sum chart 누적합(관리)도
curtailed inspection 단축검사
curtailed sampling 단축 샘플링, 단축표집
curvature 곡률
curve 곡선
curve fitting 곡선적합
curvilinear regression 곡선회귀
cutoff 절사, 버림
cutoff method 절사법
cutoff point 절사점
cutoff value 절사값, 경계값
cycle 순환, 순환마디
cycle trend 순환추세
cyclic design 순환설계
cyclic incomplete block design 순환불완비 블록 설계
cyclic order 순환 순서
cyclic permutation 순환순열, 순환치환
cyclic series 순환계열
cylinder 원기둥, 원주
cylinder set 원주집합
cylindrically rotatable design 원주형회전가능설계
damped oscillation 진폭감소진동
data 자료, 데이터
data collection 자료수집, 데이터 수집
data processing 자료처리, 데이터 처리
data sheet 자료지
death 사망
death process 사망과정
death rate 사망률
debugging 오류수정
decile 십분위수
decile deviation 십분위편차
decimal point 소수점
decimal system 십진법
decision function 결정함수
decision making 의사결정
decision procedure 결정절차
decision rule 결정규칙
decision space 결정공간
decision theory 결정이론
decomposition 분해
decreasing failure rate 감소고장률
decreasing hazard rate 감소위험률
deduction 연역, 연역법
deep stratification 심층화
defect 결점
defective 불량
defective item 불량품목, 불량품
defective proportion 불량률
defective unit 불량단위
deficiency 부족
de Finetti's theorem 드피네티의 정리
defining contrast 정의대비
definition 정의
degenerate 퇴화
degenerate distribution 퇴화분포
degree of association 연관도
degree of belief 확신도
degree of freedom 자유도
delayed renewal process 지연갱신과정
Delphi technique 델파이[델피] 기법
delta function 델타 함수
delta method 델타 방법
Deming cycle 데밍 사이클, 데밍 순환
demography 인구통계학
De Moivre's theorem 드무아브르의 정리
De Morgan's law 드모르간의 법칙
dendrogram, dendogram 나무형그림, 수목도, 덴드로그램
dense 조밀한
dense set 조밀집합
density 밀도
density function 밀도함수
denumerable 번호 붙일 수 있는, 가산의
departure process 이탈과정
dependence 종속성, 의존성
dependent 종속(적), 의존(적)
dependent event 종속사건, 종속사상
dependent variable 종속변수
depth 깊이
derivative 도함수, 미분계수
descent 하강
description 기술, 서술
descriptive statistics 기술통계(학)
descriptive survey 기술조사
design effect 설계효과, 계획효과
design matrix 설계행렬, 계획행렬
design of experiment 실험설계, 실험계획
design stress 설계 스트레스
destructive test 파괴검사
determinant 행렬식
deterministic model 결정적 모형
deterministic process 결정적 과정
deterministic simulation 결정적 모의실험, 결정적 모의시행
deviance 이탈도, 편차
diagnosis 진단
diagnostic bias 진단편향
diagonal element 대각원소
diagonal matrix 대각행렬
diagonal process 대각과정
diagonalization 대각화
diagram 도표, 다이어그램
dichotomous 이분적, 이항적, 이지(二枝)의
dichotomy 이분법
difference 차, 차분, 차집합
difference operator 차분연산자
difference set 차집합
difference table 차분표
differentiable 미분가능한
differential equation 미분방정식
differential mortality 차이사망력
differential stochastic process 미분확률과정
differentiation 미분
difficulty index 난이도
diffuse prior 확산사전(분포)
diffusion 확산
diffusion equation 확산방정식
diffusion index 확산지수
diffusion process 확산과정
dimension 차원
dimensional reduction 차원축소
direct assay 직접시험, 직접생검
direct effect 직접효과
direct product 직적, 직접곱
direct sum 직합
direction vector 방향벡터
directional data 방향자료
directional derivative 방향도함수
Dirichlet distribution 디리슈레 분포
disaggregation model 분배모형
discontinuity 불연속(성)
discontinuous 불연속인
discontinuous process 불연속과정
discordance 비부합성, 비일치성
discordant 비부합(의), 비일치(의)
discordant pair 비부합쌍, 비일치쌍
discrepancy measure 불일치측도
discrete 이산, 띄엄
discrete data 이산자료, 이산형 데이터
discrete distribution 이산분포
discrete measure 이산측도
discrete population 이산모집단
discrete power series distribution 이산멱[거듭곱]급수분포
discrete probability distribution 이산확률분포
discrete random variable 이산확률변수
discrete space 이산공간
discrete stochastic process 이산확률과정
discrete time interval 이산시구간
discrete variable 이산변수
discriminant analysis 판별분석
discriminant function 판별함수
discriminant index 변별도
disjoint events 배반사건, 서로 겹치지 않는 사건
dispersion 산포, 퍼짐(성)
dispersion index 산포지수, 퍼짐성 지수
dispersion matrix 산포행렬, 퍼짐성 행렬
dispersion stabilizing transformation 산포[퍼짐] 안정화 변환
dispersion test 산포검정[검증], 퍼짐성검정[검증]
dissimilarity 비유사성
distance 거리
distance distribution 거리분포
distributed harmonic process 분배조화과정
distributed lag 분배시차, 분포시차
distributed oscillation 분배진동
distribution 분포
distribution curve 분포곡선
distribution form 분포형
distribution-free 분포무관(한), 분포에 의존하지 않는
distribution-free sufficiency 분포무관충분성
distribution function 분포함수
distribution polygon 분포다각형
distribution table 분포표
distributive law 분배법칙
disturbance factor 교란요인
diverge 발산하다
divergence 발산
divergent 발산하는
divergent sequence 발산수열
dividing value 나누는 값, 분할값
divisibility 나누어짐
divisible 나눌 수 있는, 나누어지는
division 나눗셈
Dodge continuous sampling plan 닷지 연속 샘풀링 계획
domain 영역, 정의역
domain of convergence 수렴영역
domain of definition 정의역
domain of study 연구영역
dominant eigenvalue 지배적 고유값
dominant eigenvector 지배적 고유벡터
dominated convergence theorem 지배수렴정리
Donsker's theorem 돈스커의 정리
Doolittle technique 두리틀 기법
dose metameter 용량 메타미터
dose response 용량반응
dot graph 점그래프
dot product 스칼라 곱, 점곱
dotted line 점선
double binomial distribution 이중이항분포
double blinding method 이중눈가림방법, 이중맹검법
double confounding 이중중첩
double dichotomy 이중이분법
double exponential distribution 이중지수분포
double integral 이중적분
double k-class estimator 이중 k급 추정량
double lattice design 이중격자설계
double layer 이중층
double logarithmic chart 이중 로그 도표
double Pareto curve 이중 파레토 곡선
double periodic function 이중주기함수
double precision 이배정밀도
double reversal design 이중반전설계
double sampling inspection plan 이중 샘플링 검사계획
double sampling 이중표집, 이중 샘플링
double series 이중급수
double stochastic matrix 이중확률행렬
doubly stochastic Markov chain 이중확률 마르코프 연쇄
doubly stochastic Poisson process 이중확률 포아송 과정
doubly truncated normal distribution 이중절단정규분포
down-cross 하향교차
downward rank 하향순위
dropout 중도탈락
dual 쌍대
dual process 쌍대과정
dual scaling 쌍대척도법
dual space 쌍대공간
dual theorem 쌍대정리
dumy level 가수준
dumy treatment 가처리
dumy variable 가변수
Duncan's multiple range test 던칸의 다중범위검정[검증]
duplicated sampling 중복표집
duplication process 중복과정
durability 내구성
Durbin-Watson statistic 더빈-왓슨 통계량
dyadic system 이진법
dynamic graphics 동적 그래픽스
dynamic model 동적 모형
dynamic process 동적 과정
dynamic programming 동적 계획법
dynamic simulation 동적 모의실험, 동적 모의시행
dynamical system 동적 체계
ecological survey 생태조사
econometrics 계량경제학
economic design 경제적 설계
economic index 경제지표
economically active population 경제활동인구
Edgeworth's series 에지워스의 급수
Edgeworth expansion 에지워스 전개
effect 효과
effect size 효과크기
effective number of replication 유효반복수
effective price survey 실효물가조사
effective range 유효범위
effective unit 유효단위
efficacy 효능
efficiency 효율(성)
efficiency index 효율지수
efficient estimation 효율(적)추정
Ehrenfest model 에렌페스트 모형
eigenvalue 고유값
eigenvector 고유벡터
Eisenhart model 아이젠하트 모형
element 원소, 원
elementary contrast 기본대비
elementary event 기본사건, 근원사상
elementary probability set 기본확률집합
elementary unit 기본단위
elimination of variable 변수소거
ellipse 타원
ellipsoid 타원체
elliptic coordinates 타원좌표
elliptical normal distribution 타원형정규분포
elliptical truncation 타원형절단
elliptically contoured distribution 타원형등고선분포
elliptically symmetric distribution 타원형대칭분포
ellipticity 타원율
embedded process / imbedded process 끼워넣은 과정, 끼워진 과정
empirical Bayes estimator 경험적 베이즈 추정량
empirical Bayes procedure 경험적 베이즈 절차
empirical distribution function 경험적 분포함수
empirical likelihood 경험적 가능도
empirical probability 경험적 확률
empirical process 경험과정, 경험확률과정
empirical relation 경험적 관계
empty cell test 빈칸검정[검증]
empty event 공사건
empty set 공집합
endogenous variable 내생변수
endpoint 끝점
end-value correction 끝값수정
engineering process control 공학적 공정관리
enquete 앙케트, 여론조사
entrance time 진입시간
entropy 엔트로피
enumerable 셀 수 있는
enumeration 조사, 실사
enumeration district 조사구, 실사구
enumeration method 조사방법
enumerator 조사원
environmental heritability 환경유전
environmental statistics 환경통계(학)
epidemic model 전염모형
epidemic process 전염과정
epidemiology 역학(疫學)
equal probability selection method 등확률선택법
equal spacing test 등간격 검정[검증]
equal variance 등분산
equality 등식, 상등
equally correlated distribution 등상관분포
equally likely events 등확률사상
equation 방정식
equicontinuity 등연속
equilibrium 평형, 균형
equilibrium distribution 평형분포
equitable game 공정(한) 게임
equivalence 동등, 동치
equivalence class 동등류, 동치류
equivalence relation 동등관계, 동치관계
equivalent 동등한, 동치인
equivalent dose 동가용량
equivalent event 동등사건, 동치사건
equivalent sample 동등표본
equivariance (1) 등변성
equivariance (2) 등분산성
equivariant estimator 등변추정량
ergodic 에르고딕
ergodic Markov chain 에르고딕 마르코프 연쇄
ergodic process 에르고딕 과정
ergodic state 에르고딕 상태
ergodic theorem 에르고딕 정리
ergodicity 에르고딕성
Erlang distribution 어랑분포
error 오차
error analysis 오차분석
error function 오차함수
error graph 오차그래프
error probability 오차확률
error sum of squares 오차제곱합
error term 오차항
error variance 오차분산
errors in variable 변수내 오차
Esseen`s lemma 에씬의 보조정리
Esseen-type approximation 에씬형 근사
essentially complete class 본질적 완류비
estimable function 추정가능함수
estimate 추정값
estimated percentage error 추정백분율 오차
estimated relative error 추정 상대오차
estimating equation 추정 방정식
estimation 추정
estimation error 추정오차
estimator 추정량
Euclidean distance 유클리드 거리
Euclidean space 유클리드 공간
eugenics 생학
even function 짝함수, 우함수
even number 짝수
even permutation 짝순열, 짝치환
event 사건, 사상
evolutionary operation[EVOP] 진화적 조업[공정]
evolutionary process 진화과정
exact fit 완전적합
exact inference 정확추론
exact sampling theory 정확표집이론
exact test 정확검정[검증]
example 보기, 예
exceedance life test 초과수명검정[검증]
exceedance statistic 초과통계량
exchangeable event 교환가능사건, 호환[가능]사건
exchangeable variable 교환가능변수, 호환[가능]변수
exclusive events 배반사건, 배반사상
exhaustive events 전체를 이루는 사건들
existence theorem 존재정리
exogenous variable 외생변수
expansion 전개(식)
expansion of function in series 함수의 급수전개
expectation 기대
expected frequency 기대도수[빈도]
expected mean square 기대평균제곱
expected quality level 기대품질수준
expected value 기대값
experiment 실험
experimental design 실험설계, 실험계획
experimental error 실험오차
experimental group 실험군
experimental region 실험영역
experimental unit 실험단위
experiment-wise error rate 실험별 오류율
expert system 전문가 시스템
explanatory variable 설명변수
explicit form 명시적 형태
exploratory data analysis 탐색적 자료[데이터]분석
exploratory survey 탐색적 조사
explosive process 폭발과정
explosive stochastic difference equation 폭발적 확률차분방정식
exponential distribution 지수분포
exponential family 지수족
exponential form 지수형, 지수꼴
exponential function 지수함수
exponential growth 지수적 증가
exponential random variable 지수확률변수
exponential smoothing 지수평활
exponentially weighted moving average 지수가중이동평균
expression 식
extension 확장
extensive sampling 광역표집
exterior 외부, 바깥
exterior point 외부점, 바깥점
external criterion 외적기준
external validity 외적타당성
external variance 외부분산
externally Studentized residual 외적[외부적] 스튜던트화 잔차
extinction probability 절멸확률
extrapolation 외삽법
extra sum of squares 추가제곱합
extremal 극단(의)
extremal process 극단과정
extremal quotient 극단값 비
extremal statistic 극단통계량
exterme value distribution 극단값분포
extreme vertices design 꼭지점설계
F-distribution F 분포
F-test F 검정[검증]
face graph 얼굴그래프
factor 인자, 요인, 인수
factor analysis 인자분석
factor level 인자수준
factor loading 인자적재(값)
factor pattern 인자패턴
factor rotation 인자회전
factor score 인자점수
factorization theorem 인수분해정리
failure analysis 고장분석
failure mode 고장모드, 고장형태
failure rate 고장률
fair game 공정게임
false alarm 오경보
family 모임, 족
family of distributions 분포족, 분포모임
fast Fourire transform[FFT] 빠른 푸리에 변환
fatality rate 사망률, 치사율
Fatou`s lemma 파토우의 보조정리
feasible soiution 실현가능해
Fellegi`s method 펠레지의 방법
female reprodution rate 여성의 재생산률
Fermi-Dirac ststistics 페르미-디락 통계
Ferreri distribution 페레리 분포
fertility (in demography) 출산력, 비옥도
fetal death 태아사망
fiducial distribution 신뢰분포
fiducial inference 신뢰추론
fiducial interval 신뢰구간
fiducial limit 신뢰한계
field 장, 체, 마당
field experiment 현지실험, 현장실험
field survey 현지조사, 실사
Fiell`s theorem 피엘러의 정리
figure 도형, 그림
file 파일
filter 필터
finite 유한
finite correction 유한수정
finite difference 유한차분
finite Markov chain 유한마르코프 연쇄
finite measure 유한측도
finite population 유한모집단
finite population correction (factor) 유한모집단수정(인수, 항)
finite probability space 유한확률공간
finite sampling correction 유한표집수정
first limit theorem 제 1극한정리
first-order approximation 일차근사
first passage time 첫 통과시간
first quartile 제 1 사분위수
first return time 첫 복귀 시간
first stage unit 일단계단위
Fisher information 피셔정보
Fisher`s exact test 피셔의 정확검정[검증]
Fisher`s z-transformation 피셔의z변환
fitted value 적합값
five-number summary 다섯숫자요약, 다섯수치요약
fixed effect 고정효과, 모수효과
fixed factor 고정요인, 모수요인
fixed percent sampling 고정백분율표집
fixed point theorem 고정점정리
fixed sample size 고정표본크기
flow chart 흐름도, 순서도
fluctuation 변동
folded contingency table 접힌 분할표
folded distribution 접힌 분포
folding 접음
follow-up survey 추적조사
force of mortality 사망력
forecasting 예측
formula 공식, 식
forward difference 전진차분
forward diffusion equation 전진확산방정식
forward equations 전진방정식
forward selection method 전진선택법, 변수추가법
Fourier analysis 푸리에 분석
Fourier expansion 푸리에 전개
Fourier inversion theorem 푸리에 역변환정리
Fourier series 푸리에 급수
Fourier transformation 푸리헤 변환
fractal 프랙탈
fractile 분위수
fraction defective 불량률
fractional factorial design 부분요인설계
fractional replication 부분반복, 일부반복
Frechet distribution 프레셰 분포
free response 자유응답
freehand method 목측법
Freeman -Tukey transformation 프리만-튜키 변환
frequency 도수[빈도]
frequency curve 도수[빈도]곡선
frequency distribution 도수[빈도]분포
frequency function 도수[빈도]함수
frequency of occurrence 출현도수[빈도]
frequency polygon 도수[빈도]다각형
Fridedman`s test 프리드만의 검정[검증]
full informaton 완전정보
full-logarithm chart 완전로그 도표
fully recursive system 완전되풀이 체계
function 함수
function space 함수공간
functional 범함수
functional analysis 함수해석학
functional central limit theorem 함수적 중심극한정리
functional relation 함수관계
fundamental event 근본사건
fundamental form 근본형식
fuzzy clustering 퍼지 군집화
fuzzy probability space 퍼지 확률공간
fuzzy set 퍼지 집합
Gabriel`s test 가브리엘의 검정[검증]
gain function 이득함수
Galois field 갈루아 체
gambler`s ruin 도박꾼의 파산, 도박사의 파산
game 게임, 놀이
game theory 게임 이론
game coefficient 감마 계수
gamma distribution 감마분포
gamma function 감마 함수
gamma random variable 감마 확률변수
Gantt progress chart 간트 진행표
Gart`s test 가트의 검정[검증]
Gauss-Jordan elimination 가우스-조르단 소거(법)
Gauss-Markov theorem 가우스-마르코프 정리
Gauss-Newton method 가우스- 뉴튼 방법
Gauss-Seidel method 가우스- 사이델 방법
Gaussian curve 가우스 곡선
Gaussian density 가우스 밀도
Gaussian distribution 가우스 분포
Gaussian measure 가우스 측도
Gaussian prccess 가우스 과정
Gaussian random variable 가우스 확률변수
Geary`s ratio 기어리의 비
gene 유전자
general factor 일반인자
general inspection level 일반검사수준
generalized additive model 일반화가법모형
generalized distribution 일반화 분포
generalized inverse matrix 일반화역행렬
generalized least squares 일반화 최소제곱
generalized least squares estimator 일반화최소제곱추정량
generalized linear model 일반화선형모양
generalized logit model 일반화 로짓모형
generalized variance 일반화 분산
generating function 생성함수
generating set 생성집합
generator 생성기
genetic correlation 유전적 상관
genotype 유전자형
geometric average 기하평균
geometric Brownian motion 기하적 브라운 운동
geometric distribution 기하분포
geometric mean 기하평균
geometric probability 기하적 확률
geometric sequence 등비수열
geostatistics 지구통계학
Gibbs samlper 깁스 표집기
Gibbs sampling 깁스 표집
Gibrat distribution 지브라트 분포
Gini`s hypothesis 기니의 가설
Glejser`s regression test 글레져의 회귀검정[검증]
Glivenko-Cantelli lemma 글리벤코-칸델리 보조정리
global 대역적, 전체적
global influence 대역영향력
Gompertz curve 곰페르츠 곡선
good leverage point 좋은 지렛대점[지레점]
Goodman -Kruskal G statistic 굿맨-크루스칼 G 통계량
goodness of fit 적합도
goodness -of-fit test 적합도검정[검증]
grade 등급
gradient 기울기, 경사도
gradient method 경사법
grading 등급화, 등급매김
Graeco-Latin square 그레코-라틴 방격[정방]
Gram-Charlier series 그램-샤리에 급수
Gram-Schmidt orthogonalization 그램- 슈미트 직교화
grand mean 총평균
grand total 총계
graph 그래프, 그림
graph of broken lines 꺾은선 그래프
graphical analysis 그래프분석
graphical presentation 그래프표현
graphics 그래픽스
greatest common divisor 최대공약수
grid 그리드, 격자망
gross-error sensitivity 대형오차민감도
group 그룹, 군, 집단
group divisible 그루분할
group divisible design 그룸 분할설계
group screening method 그룹 선별법
grouped data 그룹(화)자료
grouping 그룹화
growth curve 성장곡선
Gumbel distribution 굼벨 분포
Gutman`s scale 굿트만의 척도
Hear measure 하르 척도
Hadamard matrix 하다마드 행렬
half -Cauchy distribution 절반 코쉬 분포
half-drill strip 절반파종대상(재배법)
half-normal distribution 절반 정규분포
half -normal probability paper 절반정규확률지
half-plaid square 절반격자무늬방격[정방]
half-width 절반너비, 절반폭
Hamming 해밍
Hanning 해닝
Hardy -Weinberg law 하디-와인버그 법칙
harmonic analysis 조화분석
harmonic function 조화함수
harmonic mean 조화평균
harmonic process 조화과정
Hartley's test 하트리의 검정[검증]
Hartley-Rao scheme 하트리-라오 계획
hat matrix 해트 행렬, 모자행렬
Hayek-Renyi inequality 하이엑-레니 부등식
hazard 위험
hazard function 위험함수
hazard rate 위험률
heavy-tailed distribution 두꺼운 꼬리분포
Hellinger distance 헬링거 거리
Helmert criterion 헬머트 기준
Helmert distribution 헬머트 분포
Helmert transformation 헬머트 변환
heptagonal design 칙각형설계
heritability 유전력
Hermite distribution 에르미트 분포
Hermite interpolation 에르미트 보간(법)
Hermitian form 에르미트의 형식
Hermitian matrix 에르미트 행렬
Hessian 헤시안
heterogeneity 이질성
heterogeneous 이질적
heterograde 계량형
heteroscedasticity 이분산성
heterosis 잡종강세
heterozygote 이형접합체
heuristic method 발견적 방법
hexagonal design 육각형설계
hierarchical 위계적, 계층적
hierarchical classification 위계적 분류, 계층적 분류
hierarchical clusteriong 위계적 군집화, 계층적 군집화
hierarchical model 위계모형, 계층모형
highest posterior density interval 최고사후밀도구간
hinge 경첩
histogram 히스토그램, 기둥그림표
historical series 역사적 계열
historigram 변천표
hit ratio 명중률
Hodges-Ajne's test 핫지스-에이네의 검정[검증]
Hodges bivariate sign test 핫지스 이변량 부호검정[검증]
Hodges-Lehmann estimator 핫지스-레만 추정량
Hoeffding statistic 호에프딩 통계량
Hollander's parallelism test 홀랜더의 평행성 검정[검증]
Hollander-Proschan test 홀랜더-프로샨 검정[검증]
Holt's method 홀트의 방법
homogeneity 동질성
homogeneous 동질적
homograde 계수형
homology 상동성, 호몰로지
homoscedastic 등분산적
homoscedasticity 등분산성
homozygote 동형접합체
Horvitz-Thompson estimator 호르비츠-톰슨 추정량
Hotelling's T2 호델링의 T2
household income 가계소득
Householder transform 하우스홀더 변환
housing census 주택총조사, 주택 센서스
housing unit 주택
Huber's M-estimator 후버의 M 추정량
Hunt-Stein theorem 헌트-슈타인 정리
hypergeometric distribution 초기하분포
hyper Graeco-Latin square design 그레코-라틴 방격[정방]설계
hypernormal dispersion 초정규산포
hypernormality 초정규성
hyperplane 초평면
hyper spherical normal distribution 초구형 정규분포
hypothesis 가설
hypothesis testing 가설검정[검증]
idempotent 멱등(인), 제곱이 같은
idempotent matrix 멱등행렬
identifiability 식별성
identification 식별
identification problem 식별문제
identity 항등식, 항등원, 단위원소
identity element 항등원소, 단위원소
identity matrix 항등행렬, 단위행렬
identity transformation 항등변환
iff 필요충분조건기호
ill-conditioned 불량상태의, 악조건의
illusory correlation 환영 상관
image 상, 영상
image analysis 영상분석
imbedded process / embedded process 끼워넣은 과정, 끼워진 과정
imbedding /embedding 끼워넣기
implicit form 내재적 형태
implicit function 음함수, 내재적 함수
implicit solution 음적인 해, 내재적 해
implicit strata 내재층
implicitly defined function 음적 정의함수, 내재적 정의함수
importance sampling 주표집, 중요부표집, 중요도표집
improper distribution 부적절분포, 가분포
improper solution 부적절해
imputation 대치(법)
in control 관리상태
inadmissibility 허용불가능성
inadmissible estimator 허용불가추정량
inbreeding 근친교배
incidence matrix 따름행렬
incident rate 발생률
incidental parameter 따름모수
includence test 포함관계검정[검증]
income distribution 소득분포
incomplete beta function 불완전 베타함수
incomplete block 불완비 블록
incomplete block design 불완비 블록 설계
incomplete gamma function 불완전 감마 함수
incomplete Latin spuare 불완비 라틴 방격[정방]
inconsistent equations 근을 갖지 않는 연립방정식
inconsistent estimator 불일치추정량
increasing 증가(하는)
increasing failure rate 증가고장률
increasing function 증가함수
increasing hazard rate 증가위험률
increasing index 증가지표
increasing stress 증가스트레스
increment 증분
indecomposable 분해불가능
indefinite integral 부정적분
independence 독립성
independent event 독립사건
independent increment 독립 증분
independent random variables 독립인 확률변수들
independent sample 독립표본
independent trial 독립시행
independent variable 독립변수
independently and indentically distributed 독립(적)이며 같은 분포를 따르는
index(number) 지수
index of seasonal variation 계절변동지수
indicator 지표, 표시자
indicator function 표시함수
indifference 무차별, 차이없음
indifferent zone 무차별구역, 차이없는 구역
indirect assay 간접시험, 간접생검
indirect effect 간접효과
indirect observation 간접관측
indirect sampling 간접표집
indirect survey 간접조사
individual ergodic theorem 개별 에르고딕 정리
individual index number 개별지수
individual price index 개별가격지수
individual quantity index 개별수량지수
induction 귀납
inductive behavior 귀납적 행동 [행위]
inductive definition 귀납적 정의
inductive inference 귀납적 추론
industrial classification 산업분류
inefficient statistic 비효율통계량
inequality 부등식
inequality coefficient 불평등계수
infant mortality rate 유아사망률
infective inoculation rate 감염접종율
inference 추론, 추리
infimum 하한, 최대하계
infinite 무한, 무한대
infinite decimal 무한소수
infinite dimension 무한차원
infinite limit 무한극한
infinite population 무한모집단
infinite sequence 무한수열
infinite series 무한급수
infinite set 무한집합
infinitely divisible 무한분해가능(한)
infinitesimal 무한소
infinitesimal birth rate 무한소출생률
infinitesimal death rate 무한소사생률
infinity 무한대
inflation factor 팽창인수, 팽창요인
inflection point 변곡점
influence curve 영향(력)곡선
influence function 영향(력)함수
influential observation 영향(적)관측, 주영향관측
information 정보
information matrix 정보행렬
information source 정보원
informative prior distribution 정보적 사전분포
inherent bias 내재편향
initial condition 초기조건
initial failure period 초기고장기간
initial point 초기점, 처음점
initial value 초기값
injection 단사, 일대일사상
inner array 내측배열
inner fence 안울타리
inner measure 내측도
inner product 내적, 스칼라곱
input 입력
input/output process 입출력과정
inquiry 질문조사
inspection 검사
inspection diagram 검사 다이아그램, 검사도표
inspection lot 검사로트
instantaneous death rate 순간사망률
instantaneous rate of change 순간변화율
instantaneous state 순간상태
instrumental variable 도구변수
integer 정수
integer programming 정수계획(법)
integrable 적분가능(한)
integrable function 적분가능함수
integral 적분
integral equation 적분방정식
integrand 피적분함수
integrated data 누적데이터, 통합자료
integrated moving average 누적이동평균
integrated spectrum 누적 스펙트럼
integrated squared error 적분제곱오차
integration 적분
integration by parts 부분적분
integration by substitution 치환적분
integration constant 적분상수
intensity 강도
intensity function 강도함수
intensive sampling 집중표집
interaction 상호작용, 교호작용
interaction component 상호작용성분
interaction effect 상호작용효과
interarrival time 도착간격시간
interblock 블록간
interblock estimation 블록간 추정
intereblock recovery of information 블록간 정보복구
interblock variance 블록간 분산
intercept 절편
interchange 교환
interchange theorem 교환정리
interclass correlation 급간상관, 계급간상관
interclass variance 급간분산, 계급간분산
interdecile range 십분위(간)범위
interior 내부, 안의
interior point 내부점, 안쪽 점
intermediate value theorem 중간값정리, 사이값정리
internal consiastency 내적 일치도
internal validity 내적 타당성
internally Studentized residual 내적 [내부적]스튜던트화잔차
interpenetrating sample 상호관입표본
interpoaltion 보간
interquartile range 사분위(간) 범위
interrater reliability 평정자간 신뢰도
interruption 간섭, 중단
intersection 교집합
interval 구간
interval distribution 구간분포
interval estimation 구간추정
interval scale 구간척도
intervention analysis 개입분석
intervention effect 개입효과
interview 면접
interviewer 면접자, 면접원
interviewer bias 면접자편향
intrablock 블록내
interblock estimation 블록내추정
intraclass correlation 급내상관
intraclass ratio 급내비
intraclass variance 급내분산
intrinsic accuracy 내재정확도, 고유정확도
invariance 불변성
invariance principle 불변성원리
invariant 불변량, 불변식, 불변
invariant estimator 불변추정량
inventory model 재고모형
inverse element 역원(소)
inverse estimation 역추정
inverse function 역함수
inverse Gaussian distribution 역 가우스 분포
inverse image 역상
inverse interpolation 역보간(법)
inverse matrix 역행렬
inverse moment 역적률
inverse multinomial sampling 역다항표집
inverse normal distribution 역정규분포
inverse normal scores test 역정규점수검정[검증]
inverse polynomial 역다항식
inverse probability 역확률
inverse regression 역회귀
inverse sampling 역표집
inverse serial correlation 역계열상관
inverse sine transformation 역 사인 변환
inverse transform 역변환
inversion 반전
invertibility 가역성
invertible linear transformation 가역선형변환
invertible matrix 가역행렬
invertible transformation 가역변환
inverstment coefficient 투자계수
inverstment multiplier 투자승수
irrational number 무리수
irreducible 기약, 나눌 수 없는
irreducible element 기약원
irreducible Markov chain 기약 마르코프 연쇄
irregularity 비정칙성
Irwin distribution 어원 분포
iso -cost line 등비용선
isokurtosis 등첨도
isolated system 고립 시스템
isolines 등치선
isometric chart 등거리도표
isometric mapping 등거리사상
isometric transformation 등거리 변환
isometry 등거리
isomorphism 동형사상
isotonic function 등위함수, 순서보존함수
isotonic regression function 등회귀함수
isotropic distribution 등방분포
isotropy 등방성
item 문항, 항목
item analysis 문항분석
item characteristic curve 문항특성곡선
item response theory 문항반응이론
iterated integral 반복적분
iterated linear interpolation 반복선형보간(법)
iterated logarithm 반복 로그[대수]
interated proportional fitting 반복비례적합
iteration 반복, 되풀이
iteration method 반복법
iteration trial 반복시행
iterative improvement 반복향상
iterative method 반복법
iteratively reweighted least squares 반복재가중최소제곱
J-shaped distribution J형 분포
Jackknife 잭나이프
Jacobian 야코비안, 야코비 행렬식
Jacobian determinant 야코비의 행렬식
James-Stein estimator 제임스-스타인 추정량
Jensen's inequality 젠센의 부등식
joint density 결합밀도
joint distribution 결합분포
joint frequency 결합도수[빈도]
joint independence 서로 독립, 상호독립
joint moment 결합적률
joint point 접점
joint probability density function 결합확률밀도함수
joint probability distribution 결합확률분포
joint regression 결합회귀
joint sufficiency 결합충분성
jointly continuous 공동연속, 연대연속
Jonckheere's K-sample test 죤키어의 k 표본 검정[검증]
Jordan's identity 조르단의 항등식
judgement sampling 판단표집
jump function 뜀함수, 도약함수
jump probability 뜀확률, 도약확률
just identified 적정식별
K-class estimator K급 추정량
K-sample problem K 표본문제
Kagan-Linnik-Rao theorem 카간-리닉-라오 정리
Kalman filter 칼만 필터
Kaplan-Meier esteimator 카플란-마이어 추정량
Kandall's rank correlation 켄달의 순위상관
Kandall's tau 켄달의 타우
kernel 핵
kernel estimator 핵추정량
kernel function 핵함수
key renewal theorem 핵심갱신정리
Khintchine's inequality 킨친의 부등식
Kiefer-Wolfowitz process 키퍼-월포비츠 과정
K-means clustering k 평균 군집화
knot 매듭
known quantity 기지수, 알려진 양
known term 기지항, 알려진 항
Kolmogorov axiom 콜모고로프 공리
Kolmogorov equation 콜모고로프 방정식
Kolmogorov's backward equation 콜모고로프의 후진방정식
Kolmogorov's forward equation 콜모고로프의 전진방정식
Kolmogorov-Smirnov test 콜모고로프-스미르노프 검정[검증]
KOSIS 통계정보시스템[Korean Statistical Information System]
kriging 크리깅
Kronecker delta 크로네커 델타
Kronecker product 크로네커 곱
Kruskal statistic 크루스칼 통계량
Kruskal-Wallis test 크루스칼-왈리스 검정
Kuder-Richardson formula 쿠더-리차드슨 공식
Kullback-Leibler information number 쿨백-라이블러 정보수
kurtosis 첨도, 뾰족한 정도, 뾰족함
L-statistic L 통계량
L-test L 검정[검증]
L1-estimator L1 추정량
labor cost 노동비용
labor force 노동력
labor force statistics 노동력통계
labor force survey 노동력조사
lack of fit 적합(성)결여
lack of memory 무기억성
ladder variable 사다리변수
lag 시차
lag correlation 시차상관
lag covariance 시차공분산
lag distribution 시차분포
lag effect 시차효과
lag operator 시차연산자
lag regression 시차회귀
lagred variable 시차변수
Lagrange multiplier 라그랑즈 승수
Lagrangian function 라그랑즈 함수
Laguerre polynomial 라게르 다항식
lambda-criterion 람다 기준
Laplace distribution 라플라스 분포
Laplace transform 라플라스 변환
Laplace-Levy theorem 라플라스-레비 정리
large sample 대표본
large sample approximation 대표본근사
large sample theory 대표본이론
Laspeyres' index 라스파이레스 지수
latent structure 잠재구조
latent variable 잠재변수
Latin cube 라틴입방체, 라틴 정육면체
Latin rectangle 라틴 사각형
Latin square 라틴 방격[정방, 정사각형]
Latin square design 라틴 방격[정방]설계
lattice 격자
lattice design 격자설계
lattice distribution 격자분포
lattice random variable 격자확률변수
lattice sampling 격자표집
law 법칙, 분포
law of iterated logarithm 반복 로그 법칙
law of large numbers 대수의 법칙, 큰 수의 법칙
lead time 선행시차, 선행시간, 선시차
leading diagonal 주대각(선)
leading indicator 선행지표
least absolute deviation estimator 최소절대편차추정량
least favorable 최소우호(적)
least median of squares [LMS] 최소중의제곱, 최소 메디안 제곱
least significant difference test 최소유의차검정[검증]
least square approximation 최소제곱근사
least squares estimate 최소제곱추정값
least squares method 최소제곱법
least squares smoothing 최소제곱평활
least trimmed squares [LTS] 최소절사제곱
Lebesgue integral 르베그 적분
left derivative 좌미분계수, 왼쪽미분계수
left-hand limit 좌극한, 왼쪽극한
left-hand side 좌변, 왼쪽 변
left invariant measure 좌불변측도, 왼쪽불변측도
Legendre polynomial 르장드르 다항식
Lehmann alternative 레만 대립가설[대안]
Lehman's test 레만의 검정[검증]
lemma 보조정리, 도움정리, 예비정리
leptokurtic 급첨
less or equal 이하
less than 미만
L-estimator L 추정량
lethal dose 치사용량
lethality rate 차사율
letter value display 문자값전시
letter values 문자값
level 수준
level curve 수준곡선
level line 수준선
level map 수준지도
level surface 수준면
leverage 지렛대, 지레
leverage point 지렛대점(지레점)
leverage value 지렛대값(지레값)
Levy's theorem 레비의 정리
Levy-Cramer theorem 레비-크래머 정리
lexicographical order 사전식 순서
Lexis ratio 렉시스 비
Lexis theory 렉시스 이론
Lexis variation 렉시스 변동
Liapounov's inequality 리아푸노프의 부등식
Liapounov's theorem 리아푸노프의 정리
life table 생명표
lifetime 수명
lifetime distribution 수명분포
likelihood 가능도, 우도
likelihood function 가능도함수, 우도함수
likelihood principle 가능도원리, 우도원리
likelihood ratio 가능도비, 우도비
likelihood ratio test 가능도[우도]비 검정[검증]
Likert scale 리커트 척도
limit 극한, 한계, 극한(값)
limit inferior 하극한
limit of error 오차의 한계
limit point 극한점, 집적점, 쌓인점
limit superior 상극한
limited information 제한정보
limiting distribution 극한분포
limiting moment generating function 극한적률생성함수
limiting probability 극한확률
Lindeberg-Feller theorem 린드버그-펠리 정리
Lindeberg-Levy theorem 린드버그-레비 정리
Lindley's integral equation 린들리의 적분방정식
line 선, 직선
line sampling 선표집
line spectrum 선 스펙트럼
linear 선형의
linear approximation 선형근사, 일차근사
linear combination 선형결합
linear constraint 선형제약
linear correlation 선형상관
linear dependence 선형종속
linear equation 선형방정식
linear estimator 선형추정량
linear failure rate distribution 선형고장율분포
linear form 선형형식, 일차형식
linear function 선형함수
linear functional 선형범함수
linear graph 선형 그래프, 선점도
linear hypothesis 선형가설
linear independence 선형독립성
linear interpolation method 선형보간법
linear mixed model 선형혼합모형
linear model 선형모형
linear operator 선형연산자
linear optimum estimate 선형최적추정값
linear probability model 선형확률모형
linear process 선형과정
linear programming 선형계획(법)
linear rank statistic 선형순위통계량
linear regression 선형회귀
linear regression analysis 선형회귀분석
linear space 선형공간
linear structural relation[LISREL] 선형구조관계
linear sufficiency 선형충분성
linear transformation 선형변환, 일차변환
linear trend 선형추세
linearization 선형화
linearly dependent 선형종속(인)
linearly independent 선형독립(인)
link function 연결함수
link relative index number 연결상대지수
linked blocks 연결 블록
linked paired comparison design 연결짝비교설계
linked sample 연결표본
Lipschitz condition 립쉬츠 조건
list sample 목록표본
local 국소적
local asymptotic efficiency 국소점근효율성
local average 국소평균
local control 국소제어
local influence 국소영항력
local maximum 극대, 국소최대
local minimum 극소, 국소최소
local solution 국소해
local statistic 국소통계량
local truncation error 국소절단오차
localization 국소화
locally measurable 국소(적)가측인
locally most powerful test 국소(적)최강력 검정[검증]
locally optimal design 국소(적)최적설계
locally weighted scatterplot smoothing 국소가중산점도평활
location parameter 위치모수
location-scale family of distributions 위치-척도 분포족
location shift alternative hypothesis 위치이동 대립[대안]가설
location test 위치검정[검증]
logarithm 로그, 대수
logarithmic transformation 로그 변환, 대수변환
logistic curve 로지스틱 곡선
logistic distribution 로지스틱 분포
logistic function 로지스틱 함수
logistic regression 로지스틱 회귀
logistic transformation 로지스틱 변환
logit 로짓
logit model 로짓 모형
log-likelihood function 로그 가능도 함수, 로그 우도함수
log-linear model 로그 선형모형
log-normal distribution 로그 정규분포
lognormal distribution 로그 정규분포
lognormal random variable 로그 정규확률변수
log-odds 로그 오즈
log-rank test 로그 순위검정[검증]
long tail 긴꼬리
long-term trend 장기추세, 장기경향
longitudinal survey 경시적[다시점]조사
loop 되돌림, 닫힌 곡선
Lorenz curve 로렌츠 곡선
loss function 손실함수
loss matrix 손실행렬
lot 로트, 무더기
lot inspection 로트 검사, 무더기검사
lot number 로트 번호, 무더기번호
lot quality level 로트 품질수준
lot quality protection 로트 품질보호
lot tolerance percent defective[LTPD] 로트 허용불량률
lottery sampling 복권추첨
lower bound 하한, 하계
lower control limit 관리하한
lower limit 하단, 아래끝, 아래한계, 하한
lower set 하위집합
lurking variable 잠복변수
m-dependent m 종속[의존]
M-estimation M추정
Maclaurin's expansion 매클로린 전개
magic square 마방격, 마정방
Mahalanobis distance 마할라노비스 거리
mail survey 우편조사
main block 주블록
main diagonal 주대각(선)
main effect 주효과
major defect 주결점
management information system[MIS] 경영정보시스템
Mann-Whitney U-test 만-휘트니 U검정[검증]
Mantel-Haenszel test 맨틀-핸첼 검정
mapping 사상
marginal category 주변범주
marginal classification 주변분류
marginal cost 한계비용
marginal density function 주변밀도함수
marginal distribution 주변분포
marginal homogeneity 주변동질성
marginal probability 주변확률
marginal probability function 주변확률함수
marginal productivity 한계생산성
marginal revenue 한계수익
marginal sum 주변합
marker status 혼인상태
marker variable 표시변수
market analysis 시장분석
market basket 시장바구니
market survey 시장조사
marketing research 마케팅 연구
marketing survey 마케팅 조사
Markov chain 마르코프 연쇄
Markov process 마르코프 과정
Markov property 마르코프 성질
marriage rate 혼인율
Marshall-Olkin distribution 마샬-올킨 분포
martingale 마팅게일
masking 가면화, 감춤
masking effect 가면화효과, 감춤효과
mass 무게, 질량
master sample 주표본, 마스터 표본
matched pair 대응짝
matched pairs design 대응짝설계
matched sampling 짝표집, 대응표집
matching 짝짓기, 대응
matching distribution 대응분포
maternal mortality rate 모성사망률
mathematical criminology 수리범죄학
mathematical ecology 수리생태학
mathematical expectation 수학적 기대
mathematical induction 수학적 귀납법
mathematical model 수리적 모형
mathematical probability 수리적 확률
mathematical programming 수리계획법
mathematical variable 수리적 변수
mating system 교배체계
matrix 행렬
matrix diagonalization 행렬(의) 대각화
matrix element 행렬원소
matrix sampling 행렬표집
maximal invariant 최대불변(량)
maximum 최대, 최대값
maximum likelihood 최대가능도, 최대우도
maximum likelihood estimator 최대가능도추정량, 최대우도추정량
maximum likelihood method 최대가능도방법, 최대우도법
Maxwell-Boltzmann statistic 맥스웰-볼츠만 통계량
Maxwell distribution 맥스웰 분포
McNemar's test 맥니머의 검정
mean 평균
mean absolute error 평균절대오차
mean convergence 평균수렴
mean deviation 평균편차
mean difference 평균차이
mean dispersion 평균산포
mean error 평균오차
mean integrated squared error 평균적분제곱오차
mean square approximation 평균제곱근사
mean square consistency 평균제곱일치성
mean square contingence 평균제곱우발성
mean square deviation 평균제곱편차
mean square error 평균제곱오차
mean squares 평균제곱
mean successive differences 평균연속차이
mean time between failures 평균고장시간
mean time of recurrence 평균재귀시간, 평균재발시간
mean time to failure 평균수명
mean time to repair 평균수리시간
mean value 평균값
mean value theorem 평균값정리
measurable 가측인, 잴 수 있는
measurable function 가측함수
measurable set 가측집합
measurable space 가측공간
measurable transformation 가측변환
measurable variable 가측변수
measure 측도
measure of association 연관도, 연관성측도
measure of center 중심의 측도
measure of dispersion 산포의 측도, 산포도, 퍼짐의 측도
measure of location 위치의 측도
measure of skewness 기움의 측도, 왜도
measure of variation 변동의 측도
measure space 측도공간
measure zero 측도가 영인
measurement 측정, 측량
median 중위수, 중앙값, 중간값, 메디안
median absolute deviation 충위[중간, 메디안]절대편차
median control chart 중위수관리도
median effective dose 중위수효과용량
median line 주위선, 중간선
median polish 중위수다듬기
median test 중위수검정[검증]
median unbiased 중위적 비편향(인)
membership funtion 소속함수
memoryless property 무기억성, 기억하지 못하는 성질
merge 병합, 합병
mesh 그물코
meta-analysis 메타분석
metameter 메타미터
method of elimination 소거법
method of least squares 최소제곱법
method of moments 적률법, 적률방법
method of streepest ascent [decent] 최대경사법
metric 계량(형), 거리
metric multidemensional scaling 계량형 다차원척도법
midpoint 중간점
midrange 범위의 중앙
mid-rank 중간순위
migration 이주
minimal complete class 최소완비류
minimal essential completeness 최소본질적완비성
minimal spanning tree 최소생성나무
minimal sufficient statistic 최소충분통계량
minimax 미니맥스, 최소최대
minimax estimation 미니맥스 추정
minimax principle 미니맥스 원리
minimax regret principle 미니맥스 후회원리
minimax strategy 미니맥스 전략
minimax test 미니맥스 검정[검증]
minimum 최소, 최소값
minimum chi-square estimator 최소 카이제곱추정량
mnimum deviation 최소편차
minimum mean square error estimator 최소평균제곱오차추정량
minimum variance 최소분산
minimum variance unbiased estimator 최소분산비편향추정량
minimum volum ellipsoid estimator 최소부피타원체추정량
Minkowski's inequality 민코브스키의 부등식
minor (determinant) 소행렬식
minor defect 경결점
misclassification 오분류
missing data 결측자료, 분실자료
missing value 결측값, 분실값
mixed conguential method 혼합합동법
mixed factorial experiment 혼합요인실험
mixed model 혼합모형
mixed poisson process 혼합 포아송 과정
mixed regression 혼합회귀
mixed strategy 혼합전략
mixing 혼합
mixing proportion 혼합비율
mixture 혼합물
mixture distribution 혼합분포
mixture experiment 혼합물실험
mixture model 혼합물모형
mixture of probability distribution 확률분포의 혼합
mixture random variable 혼합확률변수
modal class 최빈계급
model 모형, 모델
model diagnostics 모형진단, 모형검진
model identification 모형식별
model selection 모형선택
model transformation 모형변환
mode 최빈값
mode of distribution 분포최빈값
modified chi-square statistic 수정 카이제곱통계량
modified control limit 수정관리한계(선)
modified exponential curve 수정지수곡선
modified Gauss-Newton method 수정 가우스-뉴튼 방법
modified Latin square 수정 라틴방격[정방]
modified Newton-Raphson method 수정 라틴-라프슨 방법
modified normal distribution 수정정규분포
module 모듈
modulo 모듈로, 법
moment 적률, 모멘트
moment estimation 적률추정
moment generating function 적률생성함수
monitoring 모니터링, 감시
monotone 단조
monotone convergence theorem 단조수렴정리
monotone decreasing 단조감소
monotone function 단조함수
monotone increasing 단조증가
monotone likelihood ratio 단조가능도비, 단조우도비
monotone regression 단조회귀
monotonic function 단조함수
monotonic sequence 단조수열
monotonicity 단조성
Monte Carlo mothod 몬테칼로 방법
monthly average 월평균
Mood-Brown median test 무드-브라운 중위수검정[검증]
Moore-Penrose inverse 무어-펜로즈 역(행렬)
morbidity rate 이환률, 질병률
morbidity statistic 질병통계
Morgenstern distribution 모겐스턴 분포
mortality rate 사망률
Moses test 모제스 검정
most efficient estimator 최대효율추정량
most powerful test 최강력검정[검증]
most selective confidence interval 최대선별신뢰구간
moving annual total 이동년합계
moving average 이동평균
moving average method 이동평균법
moving average model 이동평균모형
moving frame 이동틀, 움직이는 틀
moving observer technique 이동관측자기법
moving range 이동범위
moving seasonal variation 이동계절변동
moving total 이동합계
moving weight 이동가중값
multicenter trial 다기관시험
multicollinearity 다중공선성
multi-decision problem 다중결정문제
multidimensional 다차원
multidimensional distribution 다차원분포
multidimensional scaling [MDS] 다차원척도법, 다차원척도화
multi-factor experiment 다요인실험
multi-level 다수준
multilinear process 다중선형과정
multimodal distribution 다봉분포
multinomial distribution 다항분포
multinomial random variable 다항확률변수
multinomial theorem 다항정리
multinomial trial 다항시행
multi-phase sampling 다상표집
multiple classification 다중분류
multiple comparison 다중비교
multiple correlation coefficient 다중상관계수, 중상관계수
multiple correspondence analysis 다중대응분석
multiple decision method 다중결정방법
multiple factor analysis 다중이자분석
multiple integral 중적분, 다중적분
multiple linear regression 다중선형회귀, 중선형회귀
multiple poisson distribution 다중 포아송 분포
multiple range test 다중범위검정[검증]
multiple regression 다중회귀, 중회귀
multiple smoothing method 다중평활법
multiple stratification 다중층화
multiple time series 다중시계열
multiplication law of probability 확률의 곱셈법칙
multiplicative congruential method 승법적 합동법, 승법형 합동법
multiplicative process 승법과정
multiplicative risk model 승법위험모형
multiplicity 중복도
multiplier 승수
multi-stage estimation 다단계추정
multi-stage sampling 다단계표집
multistate 다상태
multivariate 다변량
multivariate analysis 다변량분석
multivariate analysis of covariance 다변량공분산분석
multivariate analysis of variance 다변량분산분석
multivariate binomial distribution 다변량이항분포
multivariate distribution 다변량분포
multivariate exponential distribution 다변량지수분포
multivariate linear model 다별량선형모형
multivariate multinomial distribution 다변량다항분포
multivariate normal distribution 다변량정규분포
multivariate quality control 다변량품질관리
multivariate regression analysis 다변량회귀분석
multiway factorial design 다원요인설계
multiway table 다원표
mutation 돌연변이
mutually exclusive 상호배반(적)
mutually independent 상호독립(적)
natality rate 출산률
national balance sheet 국가대차대조표
natural estimator 자연추정량
natural exponential family 자연지수족
natural increase 자연증가
natural parameter 자연모수
natural parameter space 자연모수공간
natural selection 자연선택
near identification 근접식별
nearest neighbor distance 최근접이웃거리
nearest neighbor method 최근접이웃방법
negative 음의, 마이너스의
negative binomial distribution 음이항분포
negative binomial random variable 음이항확률변수
negative correlation 음의 상관
negative definite 음의 정(定)부호, 음정치
negative definite form 음의 정부호형식, 음정치형식
negative definite matrix 음의 정부호행렬, 음정치행렬
negative dependence 음의 의존성, 음의 종속성
negative exponential distribution 음지수분포
negative semi-definite matrix 음의 준정부호 행렬, 음반정치행렬
negative variation 음의 변동
nested design 지분설계
nested hypothesis 내포가설
nested model 내포모형
net effect 순효과
network 네트워크, 망, 회로망
network model 네트워크 모형
neural network 신경망
new better than used [NBU] 새것이 헌것보다 좋음
Newman-Keuls test 뉴만-쿨스 검정[검증]
Newton-Raphson method 뉴튼-라프슨 방법
Neyman allocation 네이만 배분
Neyman structure 네이만 구조
Neyman's factorization theorem 네이만의 분해정리
Neyman-Pearson lemma 네이만-피어슨 보조정리
Neyman-pearson theory 네이만-피어슨 이론
nilpotent 거듭제곱이 영인
node 마디
noise 잡음
nominal category 명목형 범주
nominal size 명목치수
nominal wage index 명목임금지수
noncentral 비중심
noncentral chi-square distribution 비중심 카이제곱분포
noncentral F-distribution 비중심 F분포
noncentral t-distribution 비중심 t분포
noncentral Wishart distribution 비중심 위샤트 분포
noncentrality parameter 비중심(성)모수
nondegenerate 비퇴화적, 퇴화되지 않은
nondegenerate matrix 비퇴화행렬
nondestructive inspection 비파괴검사
nonhomogeneous Poisson process 비동질적 포아송 과정
noninformative distribution 무정보적 분포
nonlinear 비선형
nonlinear filter 비선형 필터
nonlinear interaction 비선형상호작용
nonlinear least squares method 비선형최소제곱법
nonlinear model 비선형모형
nonlinear optimization 비선형최적화
nonlinear programming 비선형계획
nonlinear regression 비선형회귀
nonlinearity 비선형성
nonmeasurable set 불가측집합, 잴 수 없는 집합
nonmetric 비계량형
nonmetric multidimensional scaling 비계량형 다차원척도법
nonnegative definite 비음의 정부호, , 비음정치
non-normal 비정규
non-normal population 비정규모집단
nonparametric 비모수적, 비파라미터(적)
nonparametric confidence interval 비모수적 신뢰구간
nonparametric function estimation 비모수적 함수추정
nonparametric inference 비모수적 추론, 비파라미터형 추론
nonparametric method 비모수적 방법, 비파라미터적 방법
nonparametric test 비모수적[비파라미터적] 검정[검증]
nonpositive definite 비양의 정부호, 비양정치
nonrandom sample 비임의 표본
nonrandomized decision function 비임의화결정함수
nonrandomized test 비임의화검정[검증]
nonrecurrent 비재귀적, 비재발성
non-regular estimator 비정칙추정량
nonresponse 무응답, 무반응
nonsampling error 비표집오차
nonsingular 정칙, 비특이
nonsingular matrix 정칙행렬, 비특이행렬
nontrivial solution 비자명해, 자명하지 않은 해
norm 노름
normal 정규
normal approximation 정규근사
normal curve 정규곡선
normal deviate 정규편차
normal dispersion 정규산포
normal distribution 정규분포
normal distribution curve 정규곡선
normal equation 정규방정식, 표준방정식
normal family 정규족
normal inspection 보통검사
normal population 정규모집단
normal probability paper 정규확률지
normal process 정규과정
normal random variable 정규확률변수
normal score 정규점수
normality 정규성
normalization 정규화
normalized 정규화
normalized contrast 정규화대비
normalizing transformation 정규화변환
normed space 노름 공간
notation 표기
not greater than 이하
not less than 이상
not smaller than 이상
n-th order n계, n차
n-tuple n짝
nuisance parameter 장애모수
null distribution 귀무분포, 영분포
null event 영사건, 공사건
null hypothesis 귀무가설, 영가설
null matrix 영행렬
null model 영모형
null recurrent 영재귀, 귀무재귀
null recurrent state 영재귀상태, 귀무재귀상태
null set 영집합, 공집합
null space 영공간
null vector 영벡터
number theory 수론, 정수론
numeral 숫자(의)
numerator 분자
numerical 수치(의)
numerical analysis 수치해석
numerical calculation 수치계산
numerical differentiation 수치미분
numerical equation 수치방정식
numerical expression 수치적 표현
numerical instability 수치적 불안정(성)
numerical integration 수치적분
numerical method 수치적 방법
numerical solution 수치해
Nyquist frequency 니퀴스트 도수[빈도]
Nyquist interval 니퀴스트 구간
object 객체
objective function 목적함수
oblique coordinate 사교좌표
oblique projection 사교사영
oblique rotation 사각회전
observable variable 관측가능변수
observation 관측, 관측개체
observational error 관측오차
observational study 관측연구
occupancy problems 점유문제
occupation 직업
occupational classification 직업분류, 직무분류
octiles 팔분위수
odd function 홀함수, 기함수
odd number 홀수
odds 오즈, 비율비, 승산
odds ratio 오즈비 승산비
of order n n차의, n계의
ogive 누적도수[빈도]곡선
one-sided alternative hypothesis 단측대립[대안]가설
one-sided confidence interval 단측신뢰구간
one-sided hypothesis 단측가설
one-sided test 단측검정[검증]
one-step M-estimator 일단계 M 추정량
one-tailed test 한쪽꼬리검정[검증]
one-to-one 일대일
one-to-one crrespondence 일대일대응
one-to-one function 일대일함수
one-way layout 일원배치(법)
onto 위로의
onto map 위로의사상, 전사사상
open-ended question 개방형질문, 자유응답 질문
open interval 열린 구간, 개구간
open neighborhood 열린 근방
open sequential sampling scheme 열린[개]순차적 표집설계
open set 열린 집합, 개집합
operating characteristic 운영특성, 검사특성
operating characteristic curve 운영특성곡선, 검사특성곡선
operating characteristic function 운영특성함수, 검사특성함수
operation 연산
operational definition 운용정의, 조작정의
operations research [OR] 운용연구, 운용과학, O.R.
operator 연산자, 작용소
opinion survey 여론조사
opportunity loss 기회손실
optimal control 최적제이
optimal design of experiment 최적실험설계
optimal gradient method 최적경사법
optimal response condition 최적반응조건
optimal sample size 최적표본크기
optimal scaling 최적척도화
optimal score 최적점수
optimal solution 최적해
optimal stopping problem 최적정지문제
optimal stopping rule 최적정지규칙
optimality 최적성
optimization 최적화
optimum 최적
optimum allocation 최적배분(법)
optimum linear predictor 최적선형예측변수
optimum test 최적검정[검증]
order 순서, 계, 차(수)
order preserving function 순서보존함수
order property 순서성질
order relation 순서관계
order restriction 순서제약
order statistic 순서통계량
ordered alternative hypothesis 순서대립[대안]가설
ordered categorization 순서범주화
ordered n-tuple 순서있는 n짝
ordered pair 순서쌍, 순서짝
ordering 순서화, 순서매김
ordinal data 순서자료
ordinal number 순서수
ordinal scale 순서척도
ordinary least squares estimator 보통최소제곱추정량
ordinate 종좌표, 세로좌표
oriented straight line 유향직선
origin 원점
Ornstein-Uhlenbeck process 오른스타인-우렌벡 과정
orthant probability 사분면확률
orthogonal 직교
orthogonal array 직교 배열
orthogonal basis 직교기저
orthogonal central composite design 직교중심합성설계
orthogonal complement 직교여공간
orthogonal coordinate 직교좌표
orthogonal decomposition 직교분해
orthogonal design 직교설계
orthogonal function 직교함수
orthogonal matrix 직교행렬
orthogonal polynomial 직교 다항식
orthogonal polynomial regression 직교다항회귀
orthogonal projection 정사영, 직교사영
orthogonal projection matrix 정사영행렬, 직교사영행렬
orthogonal regression 직교회귀
orthogonal rotation 직교회전
orthogonal set 직교집합
orthogonal square 직교방격, 직교정방
orthogonal system 직교체계
orthogonal transformation 직교변환
orthogonality 직교성
orthogonality relation 직교관계
orthogonalization 직교화
orthonormal 직교정규
orthonormal basis 직교정규기저
orthonormal set 직교정규집합
orthonormal system 직교정규체계
orthonormalization 직교정규화
oscillation 진동
oscillatory process 진동과정
out of control 이상상태
outcome 결과, 출현
oiter array 외측배열
outer control limit 외측관리한계, 바깥관리한계
outer fence 바깥울타리
outer measure 외측도
outlier 특이점, 바깥점, 이상점
outlying value 특이값, 가깥값, 이상값
output 출력
overall estimate 총체적 추정값
overall sampling fraction 총체적 표집률
over-dispersion 과대산포
over-fitting 과대적합
overflow 넘침, 오버플로
over-identified 과대식별
overlap design 중복설계(법)
overlapping clustering 중복군집화
overlapping sampling unit 중복표집단위
over-specification 과대특정화
p-value p값
paasche's index 파아쉐의 지수
paasxhe formula 파아쉐 공식
pair 짝, 쌍
paired comparison 짝비교, 쌍(체)비교, 대응비교
paired data 짝자료, 쌍(체)자료
paired difference 짝의 차
paired observation 짝관측
paired t-test 짝(의)[쌍체] t검정[검증]
pairwise independent 짝으로[짝별로, 쌍별로]독립
palgrave's index 팔그레이브의 지수
palm function 팜 함수
palm's theorem 팜의 정리
panel 패널
panel survey 패널조사
parabolic 포물형
paradigm 패러다임
paradox 역서르 패러독스
parallel 평행(선), 나란한
parallel displacement 평행이동
parallel line 평행선
parallel line assay 평행선시험
parallel madel 병렬모형
parallel system 병렬체계, 병렬 시스템
parallel test 평행검사
parallel translation 평행이동
parallelism 평행(성)
paraparallelogram 평행사변형
parallelotope 평행체
parameter 모수, 파라미터, 매개변수
parameter design 파라미터 설계
parameter hypothesis 모수적 가설
parametric estimation 모수적 추정, 파라미터형 추정
parametric inference 모수적 추론, 파라미터형 추론
parametric model 모수적 모형, 파라미터적 모형
parametrization 매개변수화
Pareto coefficient 파레토 계수
Pareto diagram 파레토 그림
Pareto distribution 파레토 분포
Pareto index 파레토 지수
Pareto-type distribution 파레토형 분포
parsimoneous model 절약모형, 경제적 모형
part correlation 부분상관
partial 부분, 편
partial autocorrelation function 편자기상관함수
partial confounding 부분중첩, 부분혼선
partial correlation 편상관
partial correlation ratio 편상관비
partial derivative 편도함수
partial differentiable 편미분가능
partial differential 편미분
partial differential equation 편미분방정식
partial differentiation 편미분
partial enumeration 일부조사
partial F-test 편[부분] F 검정[검증]
partial inspection 일부검사
partial likelihood 편가능도, 편우도, 부분우도
partial order 부분순서
partial ordering 부분순서화
partial pivoting 부분적 축화[추축화]
partial regression coefficient 편회귀계수
partial regression plot 편회귀그림
partial replacement 부분교체
partial residual plot 편잔차그림
partial sum 부분합
partially balanced array 부분균형배열(표)
partially balanced incomplete block design 부분균형불완비블록설계
partially balanced lattice square 부분균형격자방격[정방]
partially balanced linked block design 부분균형연결블록설계
partially linked block design 부분연결블록설계
partially ordered set 부분순서집합
partition 분할, 가름
partition of chi-squared 카이제곱의 분할
partitioned matrix 분할행렬
pascal distribution 파스칼 분포
pascal's triangle 파스칼의 삼각형
passage 통로
path 경로, 길
path analysis 경로분석
path coefficient 경로계수
path diagram 경로도표
pattern 형태, 패턴
pattern recognition 형태인식, 패턴 인식
peak 정상(점)
peakedness 뾰족함
pearson's coefficient of correlation 피어슨의 상관계수
pearson curve 피어슨곡선
pearson residual 피어슨 잔차
peeling 껍질벗기기
penalized likelihood 벌점가능도
percent, percentage 백분률, 퍼센트
percent defective 불량률
percentage error 백분률오차
percentile 백분위수
perfect colinearity 완전공선성
performance characteristic 성능특성
period 주기, 기간
period analysis 주기분석
periodic function 주기함수
periodic process 주기과정
periodic replacement 주기교환, 정기교환
periodicity 주기성
periodogram 주기도
permutation 순열, 치환
permutation matrix 순열행렬
permutation test 순열검정[검증]
persistency 지속성
persistent state 지속상태
personal probability 개인적 확률
perturbation 섭동, 교란
phase 위상
phade diagram 위상도
phase function 위상함수
phase space 위상공간
phase spectrum 위상스펙트럼
phenotype 표현형
pie chare, pie diagram 파이그림, 파이도
piecewise continuous 조각별 연속
piecewise linear function 조각별 선형함수
piecewise polynomial interpolation 조각별 다항식보간법
piecewise smooth curve 조각별 평활곡선
pilot sample 시험표본
pilot survey 시험조사
Pitman alternative 피트만 대립가설[대안]
Pitman efficiency 피트만 효율
Pitman estimator 피트만 추정량
Pitman relative efficiency 피트만 상대효율
pivot 축, 추축, 중심축
pivotal quantity 축량, 추축량, 중심축량
pivoting 축화, 추축화, 중심축화
placebo 위약, 가짜약
plaid square 격자무늬방격[정방]
plane 평면
planning 계획
planning of experiment 실험계획
plot(1) 시험구, 실험구, 플롯
plot(2) 그림
plot sampling 시험구표집
point 점
point binomial distribution 점이항분포
point-biserial correlation 점이연상관
point bivariate distribution 점이변량분포
point density 점밀도
point estimate 점추정값, 점추정치
point estimation 점추정
point estimator 점추정량
point of control 관리점
point of first entry 제 1진입점
point of indifference 무차별점, 차이없는점
point of inflection 변곡점
point of symmetry 대칭점
point prediction 점예측
point process 점과정
point sampling 점표집
point set 점집합
point symmetry 점대칭
pointwise convergence 점(마다) 수렴
Poisson approximation 포아송 근사
Poisson beta distribution 포아송 베타분포
Poisson binomial distribution 포아송 이항분포
Poisson clustering process 포아송 군집화 과정
Poisson distribution 포아송 분포
Poisson index of dispersion 포아송 산포지수
Poisson model 포아송 모형
poisson probability paper 포아송 확률지
poisson process 포아송 과정
Poisson random variable 포아송 확률변수
polar 극, 극선
polar coordinate system 극좌표계
political arithmetic 정치산술
Polya's distribution 폴랴의 분포
Polya's theorem 폴랴의 정리
Polya-type frequency 폴랴형 도수[빈도]
polynomial 다항식
polynomial approximation 다항식근사
polynomial curve 다항식곡선
Polynomial interpolation 다항식보간
polynomial regression 다항식회귀
polynomial trend 다항식추세
pooled data 합동자료
pooled estimate 합동추정값
pooled sample variance 합동표본분산
pooling 합동, 합병, 통합, 병합,
pooling of classes 계급의 합동(화)
pooling of error 오차의 합동(화)
population 모집단, 인구
population census 인구총조사
population correlation coefficent 모상관계수
population defacto 사실인구, 현재인구
population dejure 상주인구, 현주인구
population density 인구밀도
population genetics 집단유전학
population parameter 모수, 모집단 파라미터
population proportion 모비율
population pyramid 인구 피라미드
population rario 모비율
population register 인구등록
population regression line 모회귀선
population standard deviation 모표준편차
population variance 모분산
portmanteau statistic 포트매토 통계량
positive 양의
positive correlation 양의 상관관계
positive definite 양의 정(定) 부호, 양정치
positive definite form 양의 정부호형식, 양정치형식
positive definite matrix 양의 정부호행렬, 양정치행렬
positive definite quadratic form 양의 정부호 이차형식
positive dependence 양의 의존성, 양의 종속성
positive semidefinite 양의 준정부호, 양반정치
positive semidefinite matrix 양의 준정부호행렬, 양반정치행렬
positive stable distribution 양의 안정분포
post cluster sampling 사후군집표집
posterior density 사후밀도
posterior density function 사후밀도함수
posterior distribution 사후분포
posterior probability 사후확률
posterior risk 사후위험
post-stratification 사후층화
postulate 공준
power (of test, 1) 검정[검증]력
power (2) 거듭곱, 멱
power curve 검정[검증]력 곡선
power function 검정[검증]력 함수
power mean 멱평균
power moment 멱적률
power of test 검정[검증]력
power series 멱급수, 거듭곱급수
power set 멱집합
power spectrum 멱 스펙트럼
power transformation 멱변환, 거듭곱 변환, 누승변환
practical significance 실제적 유의성
precedence test 선행성검정[검증]
precision 정밀도, 정도
precision prescribed 요구정밀도, 규정정밀도
predetermined variable 선결변수
prediction 예측
prediction error 예측오차
prediction interval 예측구간
prediction sum of squares 예측제곱
predictive distribution 예측분포
predictive validity 예측타당성
predictor (variable) 예측변수
preemptive discipline 우선순위원칙
preference ordering 선호도순서화
prefiltering method 사전여과법
prelimimary data 예비 데이터
preliminary survey 예비조사
preliminary test 예비검정[검증]
pre-survey 사전조사
pretest 사전검사
prevalence rate 유별율
prewhitening 사전백색화
price index 물가지수
primary sampling unit 일차표집단위
primary unit 기본단위, 일차단위
prime number 소수, 씨수
principal axis 주축
principal component analysis 주성분분석
principal component graph 주성분 그래프
principal component score 주성분점수
principal coordinate analysis 주좌표분석
principal factor analysis 주인자분석
principle 원리
principle of equipartition 등분할원리
principle of parsimony 절약성의 원리
prior distribution 사전분표, 선험적 분포
prior mean 사전평균
prior probability 사전확률, 선험적 확률
priority queueing 우선순위대기행렬
probabilistic madel 확률모형
probability 확률
probability amplitude 확률진폭
probability density 확률밀도
probability density function 확률밀도함수
probability distribution 확률분포
probability distribution function 확률분포함수
probability element 확률원소
probability function 확률함수
probability generation function 확률생성함수
probability integral transform 확률적분변환
probability mass 확룰질량
probability mass function 확률질량함수
probability measure 확룰측도
probability moment 확률적률
probability paper 확률지
probability plot 확률도, 확률플롯
probability-probability plot 확률대확률 그림
probability ratio test 확률비검정[검증]
probability sample 확률표본
probability set function 확률집합함수
probability space 확률공간
probable drror 확률오차
probit 프로빗
probit analysis 프로빗분석
probit model 프로빗 모형
probit transformation 프로빗변환
procedural bias 절차적 편향, 절차적 편의
process 과정, 공정, 프로세서
process average fraction defection 공정평균불량률
process capability 공정능력
process sapability index 공정능력지수
process capability ratio 공정능력비
process sapability value 공정능력값
process control 공정관리
processing error 처리오차
Procrustes rotation 프로크러스티즈 회전
producer's risk 생산자위험
product 곱, 적
product event 곱사건
product-limit estimator 승법극한추정량, 곱(의)극한추정량
product measure 곱측도
product moment 곱적률
product-moment correlation 곱적률상관
product multinomial distribution 곱다항분포, 적다항분포
production control 생산관리
production function 생산함수
production index 생산지수
productive capacity 생산능력
profile analysis 프로파일, 윤곽
profile plot 프로파일 그림
prognostic factor 예후요인
program 프로그램
programming 프로그래밍, 계획
programming language 프로그래밍 언어
progression 수열
projection 사영, 투영
projection matrix 사영행렬
projection operator 사영연산자, 사영작용소
projection plane 사영면, 투영면
projection pursuit 사영추적
projection pursuit regression 사영추적회귀
projective 사영적
projective transformation 사영변환
promax rotation 프로맥스 회전
proper distribution 진분포, 참분포, 적절분포
proper subset 진부분집합
proportion 비율
proportional allocation 비례배분, 비례할당
proportional constant 비례상수
proportional frequency 비례도수[빈도]
proportional hazards model 비례위험모형
proportional odds model 비례오즈모형
proportional reduction of error [PRE] 오차의 비례감소
proportional sampling 비례표집
proposition 명제
prospective study 전향적 연구
protocol 지침(서), 프로토콜
proximity 근접성, 근접도
proximity theorem 근접성 정리
proxy variable 대리변수
pseudo- 유사, 의사
pseudo-factor 유사인자
pseudo-inverse matrix 유사역행렬
pseudo-random number 유사난수
psi-function 싸이 함수
psychological scaling 심리척도화
psychometrics 계량심리학
public opinion survey 여론조사
punch card 천공카드
pure birth process 순수출생과정
pure error 순수오차
pure strategy 순수전략
purposive sample 목적표본
purposive sampling 목적표집
purposive selection 목적추출
pursuit curve 추적곡선
Q-technique Q 기법
QC circle QC 분임조
quadrant circle 사분원
quadrant dependence 사분의존성, 사분종속성
quadrat 정방[방격]구역
quadratic approximation 이차근사
quadratic estimator 이차형추정량
quadratic form 이차형태
quadratic programming 이차계획법
quadratic response 이차반응
quadratic term 이차항
qualitative data 질적자료
qualitative factor 질적요인
qualitative robustness 질적 로버스트성
qualitative variable 질적 변수, 정성변수
quality 품질
quality assurance 품질보증
quality control 품질관리
quality control chart 품질관리도
quality level 품질수준
quality specification 품질규격
quality standard 품질표준
quantal assay 가부시험
quantal response 가부반응, 계수반응
quantification method 수량화법, 수량화방법
quantification method 1 수량화 제1방법, 수량화법 1
quantification method 2 수량화 제2방법, 수량화법 2
quantification method 3 수량화 제2방법, 수량화법 3
quantification method 4 수량화 제2방법, 수량화법 4
quantification theory 수량화이론
quantile 분위수
quantile-quantile plot 분위수대분위수 그림
quantitative data 양적 자료
quantitative relative 상대수량
quantitative response 양적 반응
quantitative robustness 양적 로버스트성
quantitative variable 양적 변수
quantity 양
quartile 사분위수
quartile deviation 사분위편차
quartile measure of skewness 사분위수왜도
quartile variation 사분위변동
quasi- 준
quasi-experiment 준실험
quasi-factorial design 준요인설계
quasi-independence 준독립
quasi-Latin square 준 라틴 방격[정방]
quasi-likelihood 준가능도
quasi-Markov chain 준 마르코프 연쇄
quasi-maximum likelihood estimator 준최대가능도 추정량
quasi-Newton method 준 뉴튼 방법
quasi-normal equation 준정규방정식
quasi-random sampling 준임의표집
Quenouille's test 크누이의 검정[검증]
questionnaire 설문지
Quetelet 케틀레
queueing problem 대기행렬문제
queueing process 대기행렬과정
queueing theory 대기행렬이론
quintiles 오분위수
quota method 할당법
quota sampling 당표집
R-estimator R 추정량
R-technique R 기법
radix 기수
Radom-Nikodym derivative 라돈-니코딤 도함수
random 임의, 랜덤, 무작위, 확률(적)
random arrangement 임의배치, 확률적 배치
random censoring 임의중도절단
random component 임의성분, 랜덤성분
random distribution 임의분포, 확률분포
random effect 임의효과, 변량효과
random error 임의오차, 랜덤오차, 확률오차
random event 임의사상, 확률사상
random experiment 임의실험, 확률실험
random failure 우발고장
random field 임의장, 확률장
random impulse process 임의충격과정, 확률충격과정
random interval 임의구간, 확률구간
random lines graph 임의선 그래프
random mating 임의교배, 랜덤 교배
random motion 임의운동
random number 난수, 임의수
random number die 난수주사위
random number table 난수표
random order 임의순서, 랜덤순서
random process 임의과정, 확률과정, 랜덤과정
random sample 임의표본, 확률표본, 랜덤표본
random sampling 임의표집, 확률표집
random search 임의탐색
random variable 확률변수
random vector 확률벡터
random walk 임의보행, 확률보행
random zero 임의영
randomization 임의화, 확률화, 랜덤화
randomization model 임의화모형
randomization test 임의화검정[검증}, 확률화검정[검증]
randomized block design 임의화[랜덤화, 확률화] 블록 설계
randomized decision function 임의화[확률화]결정함수
randomized response 임의화응답, 확률화응답
randomized trial 임의화시행, 확률화시행
randomness 임의성, 확률성, 우연성
range 범위, 치역
range control chart 범위관리도
rank (1) 순위
rank (2) 계수(階數)
rank condition of identification 식별계수조건
rank corretion 순위수정
rank correlation 순위상관
rank-sum test 순위합검정[검증]
ranking method 순위화방법
Rao's scoring test 라오의 점수화검정[검증]
Rao-Blackwell theorem 라오-블랙웰 정리
Rasch model 라쉬 모형
rate 율
rate of change 변화율
rate of increment 증가율
rating method 평정방법
rating-score method 평정점수법
ratio 비, 율
ratio estimator 비추정량
ratio scale 비척도
rational number 유리수
raw data 원자료
raw material 원재료
raw moment 원적률
Rayleigh distribution 랄리 분포
Rayleigh test 랄리 검정[검증]
real function 실합수
real number 실수
real variable 실변수
real wage index 실질임금지수
realization 실현
rearrangement 재배열
recessive 열성
reciprocal 역(의), 서로간의
reciprocal average method 교호평균볍
reciprocal transformation 역변환
recognition 인지, 인식
records test 기록값검정[검증]
rectangle 직사각형
rectangle graph 직사각형 그래프
rectangular association scheme 직사각동반계획
rectangular coordinate system 직교좌표계
rectangular distribution 직사각형분포
rectangular lattice 직사각격자
rectified index number 교정지수
rectilinear trend 직선적 경향
recurrence time 재귀시간, 재발시간
recurrent 재귀적, 재발성
recurrent Markov chain 재귀적 마르코프 연쇄
recurrent state 재귀(성) 상태
recursion 되풀이, 순환, 반복
recursion formula 점화식
recursive 되풀이하는
recursive function 되풀이체계
recursive system 되룰이체계
reduced form 축소형
reduced form equations 축소형방정식
reduced inspection 축소검사, 수월한 검사
reduced scale 축척
reduced variate 축소변량
reduction 축소, 약분, 축약
reduction of order 차수의 축소
redundancy 과잉, 중복
re-expression 재표현
reference period 준거기간
reference scale 준거척도, 기준자
reference set 준거집합
reference year 준거년, 기준년,
reflecting barrier 반사벽
reflexive 반사적
reflexive relation 반사관계
refusal rate 거부율
regeverative process 재생성과정
region 영역
region of interest 관심영역
regional statistics 지역통계
regressand 피회귀변수
regression 회귀
regression analysis 회귀분석
regression coefficient 회귀계수
regression curve 회귀곡선
regression diagnostics 회귀진단, 회귀검진
regression equation 회귀식
regression estimate 회귀추정값
regression line 회귀선, 회귀직선
regression mean squares 회귀평균제곱
regression model 회귀모형
regression plane 회귀평면
regression spline 회귀 스풀라인
regression straight line 회귀직선
regression through the origin 원점통과회귀, 원점회귀
regressor 회귀변수
regret 후회, 기회손실
regular estimator 정칙추정량
regular matrix 정칙행렬
regularity condition 정칙조건
reject 기각하다
rejectable quality level 불합격품질수준
rejection 기각
rejection error 기각오류
rejection number 기각수, 불합격판정수
rejection region 기각역, 기각영역
rejective sampling 기각표집
relation 관계
relational model 관계형모형
relative accuracy 상대정확도
relative dispersion 상대산포도
relative efficiency 상대효율
relative error 상대오차
relative frequency 상대도수[빈도]
relative index 상대지수
relative information 상대정보량
relative potency 상대효능
relative precision 상대정밀도
relative probability 상대확률
relative risk 상대위험도
relative variance 상대분산
relaxed oscillation 완화진동
reliability 신뢰성, 신뢰도
reliability analysis 신뢰도분석
reliability coefficient 신뢰도, 신뢰성계수
reliability curve 신뢰도곡선
reliability engineering 신뢰성공학
reliability function 신뢰도함수
remainder 나머지, 잔차
renewal 갱신, 재생, 다시 새로움
renewal distribution 갱신분포
renewal equation 갱신방정식
renewal process 갱신과정, 다시 새로움 과정
renewal rate 갱신률
renewal theorem 갱신정리
repair 수리
reparametrization 재모수화
repeatability 반복(가능)성
repeated combination 중복조합
repeated measurement 반복측정
repeated permutation 중복순열
repeated sampling 반복표집
repeated signficance test 반복유의성검정[검증]
repeated survey 반복조사
repeated trial 반복시행
repetiton 반복
replacement 복원
replacement cost 교체비용
replicated sampling 반복표집, 반복 샘플링
replication 반복
representative sample 대표(적)표본
representative value 대표값
reproducibility 재현(가능)성
resampling 재표집
research hypothesis 연구가설
residual 잔차
residual effect 잔류효과
residual lifetime 잔여수명
residual sum of squares 잔차제곱합
residual variance 잔차분산
residual vector 잔차 벡터
residual waiting time 잔여대기시간
resistance 저항성
resistant line 저항직선, 저항성직선
resolution 해상도
resolvable design 분해가능설계
respondent 응답자
response 반응, 응답
response error 반응오차, 응답오차
response function 반응합수
response metameter 반응메타미터
response surface analysis 반응표면분석
response surface design 반응표면설계
response time distribution 반응시간분포
response variable 반응변수
restricted randomization 제한임의화, 제한확률화
restricted regression 제한회귀
restricted sequential procedure 제한적 순차절차
retail price index 소매물가지수
retrospective study 후향(적)연구
return period 복귀주기
return time 복귀시간
reversal design 반전설계
reversal test 반전검정[검증]
reverse 역
reversible relation 가역관계
reweighted least squares 재가중최소제곱
ridge estimator 능선추정량, 능형추정량
ridge regression 능선회귀, 능형회귀
ridge trace method 능선추적법, 능형추적법
Riemann distribution 리만 분포
Riemann integral 리만 적분
Riemann-Lebesgue theorem 리만-르베그 정리
right inverse 오른쪽역원, 우역원
right invertible 오른쪽가역, 우가역
rigid mition 강체운동
risk 위험
risk function 위험함수
risk set 위험집합
robust 로버스트
robust design 로버스트 설계
robust inference 로버스트 추론
robust method 로버스트 방법
robustness 로보스트성
root mean square error 제곱근평균제곱오차
rotatable design 회전기능설계
rotating coordinates method 회전좌표법
rotation 회전, 순환
rotation sampling 순환표집, 교체표집
Rothamsted Experimental Station 로담스테드 시험장
rough 거칠음, 잔차
rough estimation 어림추정
round number 어림수
round-off error 반올림오차
round-robin design 라운드-로빈 설계
rounding 반올림
rounding error 반올림오차
rounding off 버림
rounding off error 버림오차
rounding up 올림
route sampling 도로표집
row 행
row vector 행벡터
ruler 자
run 런, 연, 연속마디
run length 런 길이, 연길이
run test 런 검점[검증], 연검정[검증]
running mean 이동평균
running median 이동중위수
saddle point 안장점, 안부점
sample 표본
sample allocation 표본배분
sample distribution function 표본분포함수
sample fluctuation 표본변동
sample inspection 표본검사
sample line 표본선
sample mean 표본평균
sample range 표본범위
sample size 표본(의) 크기
sample space 표본공간
sample standard deviation 표본표준편차
sample statistic 표본통계량
sample survey 표본조사
sample survey techniques 표본조사기법
sample variance 표본분산
sampled population 표집모집단
sampling 표집, 추출, 표본추출, 샘플링
sampling bias 표집편향, 표집편의
sampling card 표집카드, 샘플링 카드
sampling design 표집설계
sampling distribution 표집분포
sampling error 표집오차
sampling for attributes 속성형샘플링
sampling fraction 표집률, 추출률
sampling frame 표집률
sampling inspection 샘플링 검사, 표집검사
sampling inspection by attributes 계수형 샘플링 검사
sampling inspection by variables 계량형 샘플링 검사
samlpling interval 표집간격, 추출간격
samlpling plan 표집계획
sampling survey 표집조사
sampling unit 표집단위
sampling variation 표집변동
sampling with equal probability 등확률표집
sampling with probability proportional to size 크기비례확률표집
sampling with replacement 복원표집, 복원추출
sampling without replacement 비복원표집, 비복원추출
sampling zero 표집영
saturated 포화(된)
saturated model 포화모형
saturation 포화
Savage test 쎄비지 검정[검증]
scalar 스칼라
scale 척도, 눈금
scale invariance 척도불변성
scale parameter 척도모수
scale transformation 척도변환
scaled deviance 척도(화)이탈도[편차]
scaling 척도화
scatter coefficient 산포계수
scatter plot, scatter diagram 산점도
scatter plot matrix 산점도행렬
Scheffe's test 쉐페의 검정[검증]
Schwarz's inequality 슈바르츠의 부등식
score 점수
score function 점수함수
scoring method 점수화방법
scree graph 산비탈그림, 스크리 그래프
screening 선별
screening design 선별설계
screening inspection 섬별검사
search method 탐색법
seasonal adjustment 계절조정
seasonal factor 계절인수, 계절요인
seasonality 계절성
seasonal variation 계절변동
secondary analysis 이차분석
secondary attack rate 이차발병률
secondary data source 이차자료원
secondary sampling unit 이차표집단위
secondary unit 이차단위
section 단면, 자른면
seemingly unrelated regression[SUR] 겉보기 무관[보기에 무관한]회귀
segmentation 세분화
segmented polynomial regression 구간별다항회귀
selection 선택, 선발
selection bias 선택편향
selection index 선발지수, 선택지수
self-administered questionnaire 자기기입식설문지, 자기식설문지
self-conjugate Latin square 자기컬레[공액]라틴 방격[정방]
self fertilization 자가수정
self similar process 자기유사과정
semi- 준, 반
semi-continuous 준연속
semi-definite quadratic form 준정부호이차형식
semi-finite measure 준유한측도
semi-invariant 준불변
semi-invariant coefficient 준불변계수
semi-Markov process 준 마르코프 과정
semi-martingale 준마팅게일
semiparametric method 준모수적 방법, 준파라미터적 방법
sensitivity 민감도
sensory evaluation 감각평가, 관능평가
sensory test 감각검사, 관능검사
separable 분리가능한
separable set 분리가능집합
separable space 분리가능공간
separation 분리
sequence 수열, 열
sequential 순차(적), 축차(적)
sequential analysis 순차(적)분석
sequential decision problem 순차적 결정문제
sequential design 순차설계
sequential estimation 순차추정
sequential experiment 순차실험
sequential inspection 순차검사
sequential probability ratio test 순차확률비검정[검증]
sequential sampling 순차표집
sequential test 순차(적)검정[검증]
serial correlation 계열상관
serial lag correlation 계열시차상관
serial variation 계열변동
series 급수, 계열
series model 직렬모형
series system 직렬체계, 직렬 시스템
set 집합
set function 집합함수
set operation 집합연산
set theory 집합론
sex chromosome 성염색체
sex linkage 성연관
sex ratio 성비
sex structure 인구성별구조
shape analysis 형상분석, 형태분석
shape parameter 형상모수, 형태모수
shape restriction 형상제약, 형태제약
Shapiro-Wilk test 샤피로-윌크 검정
Sheppard's correction 쉐파드의 수정
Shewhart control chart 슈하트 관리도
shift 이동, 밀림
shift parameter 이동모수
shock model 충격모형
short-term fluctuation 단기변동
shortest confidence interval 최단신뢰구간
shortest prediction interval 최단예측구간
shrinkage estimater 축소추정량
sigmoid curve 시그모이드 곡선
signal 신호
sigmal-to-noise ratio 신호대잡음 비
sign 부호
sign test 부호검정[검증]
signed measure 부호측도, 부호가 붙은 측도
signed rank test 부호순위검정[검증]
significance 유의성
significance level 유의수준
significance probability 유의확률
significance test 유의성검정[검증]
significant 유의적, 유의한
similar action 유사행동, 유사행위
similar region 유사영역, 닯은 영역
similar test 유사검정[검증], 닯은 검정[검증]
similarity 유사성, 상사성, 닯음
simple hypothesis 단순가설
simple index number 단순지수
simple interaction 단순상호작용
simple lattice 단순격자
simple lattice design 단순격자설계
simple random sample 단순임의[단순랜덤, 단순확률]표본
simple random sampling 단순임의[단순랜덤, 단순확률]표집
simple randomization 단순임의화[랜덤화, 확률화]
simple regression 단순회귀
simple regression model 단순회귀모형
simple structure 단순구조
simplex 심플렉스
simplex centroid design 심플랙스 중심설계
simplex design 심플렉스 설계
simplex lattice design 심플렉스 격자설계
simplex method 심플렉스법
simplex screening design 심플렉스 선별설계
simplex search method 심플렉스 탐사법
Simpson's paradox 심프슨의 역설, 심프슨의 패러독스
simulation 모의실험, 시물레이션 , 모의시행
simulation experiment 모의실험
simulator 모의 실험기, 모의시행기
simultaneous 동시(적)
simultaneous confidence interval 동시신뢰구간
simultaneous equations 연립방정식
simultaneous equations model 연립방정식 모형
simultaneous inference 동시추론
single equation estimation 단일방정식 추정
single factor experiment 단일요인실험
single factor theory 단일인자이론
single linkage 단일연결(법)
single precision 단일정밀도
single sampling inspection 일회 샘플링 검사
single sampling plan 일회 샘플링 계획
singlecton 한원소집합
singular 비정칙, 특이
singular distribution 특이분포
singular matrix 비정칙행렬, 특이행렬
singular measure 특이측도
singular value 비정칙값, 특이값
singular value decomposition 비정칙값분해, 특이값분해
six point assay 여섯점시험, 육점시험
size 크기
size distribution 크기분포
size of a test 검정[검증]의 크기
size of class interval 계급구간의 크기
skew symmetric 반대칭
skew symmetric matrix 반대칭행렬
skewed distribution 기운 분포
skewness 왜도, 기움, 비대칭도
sliced inverse regression 분할역회귀
slippage model 미끄러짐 모형
slippage test 미끄러짐 검정[검증]
slope 기울기
slope of regression line 회귀직선의 기울기
slope ratio assay 기울기비시험
Slutzky process 슬럿츠키 과정
Slutzky-Yule effect 슬럿츠키-율 효과
small-area statistics 소지역통계
small sample 소표본
small-sample theory 소표본이론
Smirnov test 스미르노프 검정
smooth 매끄러운
smooth curve 평활곡선, 매끄러운 곡선
smoother 평활기
smoothing 평활(화), 매끄럽게함
smoothing coefficient 평활계수
smoothing method 평활(방)법
smoothing parameter 평활모수, 평활 파라미터
smoothing power 평활력
smoothness 평활도, 매끄러움
social desirability bias 사회적 요망성 평향
social indicator 사회지표
social research 사회연구
social survey 사회조사
socio-economic status 사회경제적 지위
sociometrics 계량사회학
software 소프트웨어
sojourn time 체류시간
solution 해, 풀이
sorting 순서화, 크기순정렬
source 출처, 원천
source of variation 변동요인
space 공간
span 생성, 펼침
spanned 생성된
sparse 희박한
sparse matrix 희박(한) 행렬
spatial data 공간자료
spatial distribution 공간분포
spatial pattern 공간패턴, 공간형태
spatial point process 공간점과정
spatial process 공간과정
spatial statistics 공간통계(학)
spatial systematic sample 공간계통표본
Spearman's rho 스피어만의 로
Spearman-Brown formula 스피어만-브라운 공식
special purpose survey 특수목적조사
specification 특정화, 규격
specification error 특정화의 오류, 규격오류
specification limit 규격한계
specification of quality 품질규격
specific variance 특정분산
specificity 특이도, 특정율
specimen 시제품
spectral decomposition 스펙트럼 분해
spectral density 스펙트럼 밀도
spectral density function 스펙트럼 밀도함수
spectral function 스펙트럼 함수
spectral measure 스펙트럼 측도
spectral weight function 스펙트럼 가중치함수
spectral window 스펙트럼 원도우
spectrum 스펙트럼
Spencer formula 스펜서 공식
spent waiting time 소모대기시간
sphere 구, 구면
spherical distribution 구형분포, 구면분포
spherical normal distribution 구형정규분포
spherical polar coordinate 구면극좌표
spherical triangle 구면삼각형
spherical variance function 구형분산함수
sphericity test 구형성검정[검증]
spline 스플라인
spline function 스플라인 함수
spline interpolation function 스플라인 보간함수
split 분할
split-half method 반분법
split-half reliability coefficient 반분신뢰도
split-plot confounging 분할구중첩
split-plot design 분할구설계
split-plot error 분할구오차, 세구오차
split-split-plot design 세세구설계
spurious correlation 허위상관, 가짜상관
square 정사각형, 제곱, 방격, 정방
square lattice 정방형격자, 정사각형격자
square matrix 정방행렬, 정사각형행렬
square root transformation 제곱근변환
squared error 제곱오차
stability 안정성
stability test 안정성검정[검증]
stable 안정된
stable distribution 안정분포
stable process 안정과정
stable state 안정형태
stacking 쌓기
Stacy's distribution 스테이시의 분포
staircase design 계단식설계
standard 표준
standard Browning motion 표준 브라운 운동
standard classification 표준 분류
standard deviation 표준편차
standard error 표준오차
standard form 표준형
standard industrial classification 표준산업분류
standard Latin square 표준 라틴 방격[정방]
standard measure 표준측도
standard normal distribution 표준정규분포
standard population 표준모집단
standard score 표준점수
standardization 표준화
standardized mortality ratio 표준화사망률
standardized regression coefficient 표준화회귀계수
standardized residual 표준화잔차
standardized variable 표준화변수
star plot 별그림
state 상태
state of statistical control 통계적 관리상태
state space 상태공간
state space representation 상태공간표현
static model 정태모형
static simulation 정태적 모의실험, 정태적 모의시행
static statistic 정태통계량
stationary condition 정상조건
stationary distribution 정상분포
stationary population 정상인구
stationary process 정상과정, 시불변과정
stationary stochastic process 정상확률과정
stationary time series 정상시계열
stationary 정상(적), 시불변(적), 정류(적)
statistic 통계량
statistical analysis 통계분석
statistical consultant 통계상담인
statistical control 통계적 관리
statistical curvature 통계적 곡률
statistical data 통계자료
statistical database 통계 데이터베이스
statistical design 통계적 설계
statistical diagram 통계도표
statistical estimation 통계적 추정
statistical function 통계적 범함수
statistical graphics 통계 그래픽스
statistical hypothesis 통계적 가설
statistical inference 통계적 추론
statistical law 통계법칙
statistical map 통계지도
statistical matching 통계적 짝짓기
statistical metric space 통계적 거리공간
statistical model 통계적 모형
statistical package 통계 팩키지
statistical population 통계적 모집단
statistical prediction 통계적 예측
statistical probability 통계적 확률
statistical process control [SPC] 통계적 공정관리
statistical quality control [SQC] 통계적 품질관리
statistical series 통계계열
statistical significance 통계적 유의성
statistical survey 통계조사
statistical table 통계표
statistical tolerance interval 통계적 허용구간
statistical tolerance limit 통계적 허용한계
statistical tolerance region 통계적 허용역
statistically equivalent block 통계적 동등 블록
statistician 통계전문가, 통계전문인
statistics 통계학
statistics of attributes 속성(형)통계
statistics of variables 변수(형)통계
statistics of variates 변량(형)통계
steady state 안정상태
steepest ascent method 최대상승법, 최대경사법
steepest descent method 최대하강법, 최대경사법
stein estimator 스타인 추정량
stein's two sample procedure 스타인의 이[2]표본절차
stem-and-leaf display 줄기-잎 전시[그림]
stem plot 줄기그림
step 계단, 단계
step function 계단함수
step stress testing 계단 스트레스 시험
stepwise regression 단계별 회귀
stepwise selection 단계별 선택
stereogram 입체 그래프
stieltjes' integral 스틸체스 적분
stimulus 자극
sterling distribution 스털링 분포
stochastic 확률적
stochastic approximation 확률근사
stochastic approximation procedure 확률적 근사절차
stochastic continuity 확률적 연속성
stochastic convergence 확률적 수렴
stochastic dependence 확률적 의존성. 확률적 종속성
stochastic differentiability 확률적 미분가능성
stochastic differential equation 확률미분방정식
stochastic independence 확률적 독립성
stochastic integrability 확률적 적분가능성
stochastic integral 확률적 적분
stochastic kernel 확률핵
stochastic matrix 확률행렬
stochastic model 확률적 모형
stochastic ordering 확률적 순서화
stochastic process 확률과정. 임의과정
stochastic programming 확률계획법
stochastic simulation 확률적 모의실험, 확률적 모의시행
stochastic system 확률 시스템, 확률적 체계
stochastic variable 확률(적)변수
stochastically larger(smaller) 확률적으로 큰(작은)
stopping rule 정지규칙
stopping time 정지시간
strata chart 계층도
strategy 전략
stratification 층화
stratified multi-stage sampling 층화다단표집
stratified one-stage sampling 층화일단표집
stratified random sampling 층화임의표집
stratified sampling 층화표집, 층별표집
stratum 층
stress 스트레스, 부하
stress-strength model 스트레스-강도모형
stressing rate 부하율
strict partial order 순부분순서
strictly convex 순볼록
strictly increasing 순증가
strictly increasing function 순증가함수
strictly positive number 순양수
strictly stationary process 순정상과정, 협의의 정상과정
strong completeness 강완비성
strong law of large numbers 대수의 강법칙, 큰 수의 강법칙
strong Markov property 강 마르코프 성질
strong mixing property 강혼합성질
strongly consistent estimator 강일치추정량
strongly stationary process 강정상과정
structural equation 구조방정식
structural relationship 구조적 관계
structural zero 구조적 영
structure 구조
structured question 구조화질문
Student's distribution 스튜던트의 분포
Student's t-statistic 스튜던트의 t 통계량
Studentized range 스튜던트화 범위
Studentized residual 스튜던트화 잔차
Sturges' rule 스터지스의 법칙
subadditivity 준가법성
subexponential distribution 열(劣)지수분포
subgroup 부분군
subjective probability 주관적 확률
submartingale 열(劣) 마팅게일, 서브마팅게일
subminimax 부최대최소
subnormal dispersion 열(劣)정규산포
sub-poisson distribution 열(劣)포아송 분포
subpopulation 부모집단
sub-sample 부표본
sub-sampling 부표집
subset 부분집합
subset selection method 부분집합선택방법
subspace 부분공간
substitution 대입, 치환
substratification 부층화, 부차층화
sub-sub sampling 부부차 표집
sucessive difference 연속차분
sufficiency 충분성
sufficient statistic 충분통계량
Sukhatme's test 수카트미의 검정[검증]
sum 합
sum of squares 제곱합
superefficiency 초효율성
supermartingale 초[우, 優] 마팅게일, 수퍼 마팅게일
supernormal dispersion 초정규산포
superpopulation 초모집단
supplementary 보조(적), 보적의
support 받침, 지지
supremum 상한, 최소상계
surface 표면
survey 조사
survey design 조사설계
survival analysis 생존분석
survival function 생존함수
survival probability 생존확률
survival rate 생존률
swamp effect 수렁효과
sweeping method 쓸어내기 방법
switch back design 전환설계
switching regression 교체회귀
symmetric 대칭(적)
symmetric difference 대칭적 차이
symmetric event 대칭사건
symmetric function 대칭함수
symmetric matrix 대칭행렬
symmetric sampling 대칭표집
symmetric stable law 대칭안정분포
symmertic transformation 대칭변환
symmetric transposition 대칭이동
symmertical circular distribution 대칭원형분포
symmetrical displacement 대칭이동
symmetrical distribution 대칭분포
symmetrical factorial design 대칭요인설계
symmetrical test 대칭검정[검증]
symmetrical unequal bblock arrangement 대칭불균등불록배열
symmetry 대칭성
sympathy effect 동정효과
system 시스템, 체계
systematic 계통적, 체계적
systematic component 체계적 성분
systematic design 체계적 설계
systematic error 계통오차
systematic sampling 계통표집, 계통추출
t-distribution t 분포
t-score t 점수
t-test t 검정[검증]
tabulated data 제표자료
tabulation 제표
Taguchi method 다구치 방법
tail event 꼬리사건
Takacs process 타칵스 과정
target population 목표 모집단
target value 목표값
taxonomy 분류(학)
Taylor expansion 테일러 전개
Tchebychev inequality 체비세프 부등식
telephone survey 전화조사
tensor 텐서
tensor product 텐서 곱
term 항
terminal decision 단말결정
Terry-hoeffding test 테리-호에프딩 검정[검증]
test (1) 검정, 검증
test (2) 시험, 검사
test equating 시험등화
test function 시험함수
test of goodness-of-fit 적합도검정[검증]
test of homogeneity 동질성검정[검증]
test of hypothesis 가설검정[검증]
test of independence 독립성검정[검증]
test of normality 정규성검정[검증]
test of statistical hypothesis 통계적 가설검정[검증]
test-retest reliability 검사-재검사 신뢰성[신뢰도]
test size 검정[검증]의 크기
test statistic 검정[검증]통계량
test survey 시험조사
testing until a truncated time 정시중단검사
testing until r items fail 정수중단검사
tetrachoric correlation coefficient 사분상관계수
thin-tailed distribution 얇은 꼬리 분포
third quartile 제3 사분위수
Thompson's rule 톰슨의 규칙
three dimensional lattice 삼차원격자
three-factor interaction 삼요인상호작용
therr-mode factor analysis 삼상인자분석
three point assay 삼점시험
three series theorem 삼급수정리
three stage least squares [3SLS] 삼단계최소제곱
three-stage sampling 삼단계표집
three-way factorial design 삼원요인설계
three-way multidimensional scaling 삼원다차원척도법
threshold 분계점
Thurstone scale 써스톤 척도
ticket sampling 티켓 표집, 티켓 추출(법)
tied ranks 등순위, 동순위
tightened inspection 엄격검사, 까다로운 검사
time dependent 시간의존적인
time lag 시차
time plot 시도표
time reversible 시간역류가능, 시간역류성
time series 시계열
time series analysis 시계열분석
time series plot 시계열그림
tolerance 허용, 공차
tolerance design 공차설계
tolerance interval 허용구간
tolerance limit 허용한계, 공차한계
tolerance region 허용영역, 공차영역
topology 위상, 위상수학
total children born 총출생아수
total correlation 총상관
total inspection 전수검사
total quality control 전사적 품질관리
total sum 총계
total time on test 총검사시간
total variation 총변동
toxicity 독성
toxicoligy 독성학
trace 대각합
trancefer function 전이함수
transform, transformation 변환
transformation set 변환집합
transient 일시적, 경과적
transient state 일시(적)상태, 일시성 상태
transition matrix 전이행렬, 추이행렬
transition probability 전이행렬, 추이확률
translation 이동, 평행이동
translation equivariance 이동등변성
translation invariance 이동불변성
translation parameter 이동모수
transmission rate 전달률
transpose 전치
transpose of a matrix 행렬의 전치
transposed matrix 전치행렬
transpisition 호환, 자리바꿈, 이항
transposition matrix 호환행렬
treatment 처리
treatment combination 처리조합
treatment contrast 처리대비
tree graph 수형도, 나무가지그림
trend 추세, 경향
trend fitting 추세적합
trend line 추세선
trial 시행, 시험, 실험
trial and error 시행착오
triangular association scheme 삼각동반계획
triangular design 삼각설계
triangular distribution 삼각형분포
triangular inequality 삼각부등식
triangular matrix 삼각행렬
trimean 삼평균
trimmed mean 절사평균
trimming 절사
trinomial 삼항(의)
trinomial distribution 삼항분포
triple lattice 삼중격자
trivariate 삼[3]변량
triveal solution 자명해
trough point 계곡점
truncate 절단하다
truncated distribution 절단분포
truncated normal distribution 절단정규분포
truncated regression 절단회귀
truncated sampling 절단표집
truncation 절단
truncation error 절단오차
Tukey statistic 튜키 통계량
tuning constant 조율상수
turning point 전환점
twinned distributions 쌍둥이분포
two dimensional lattice 이차원격자
two dimensional table 이차원표
two-factor interaction 이요인상호작용
two-factor theory 이인자이론
two-level factorial design 이수준요인설계
two person game 이인 게임
two-phase sampling 이상표집
two-point assay 이점시험
two sample problem 이표본문제
two sample test 이표본검증[검정]
two-sided hypothesis 양측가설
two-sided test 양측검정[검증]
two-stage estimator 이단계추정량
two-stage least squares[2SLS] 이단계최소제곱
two-stage sampling 이단계표집
two-tailed test 양쪽꼬리검정[검증]
two-way design of experiment 이원실험설계
two-way factorial design 이원요인설계
two-way layout 이원배치법
type A distribution A형 분포
type A series A형 급수
type B distribution B형 분포
type B series B형 급수
type Ⅰ distribution 제1종 분포
type Ⅰ error 제1종 오류
type Ⅱ distribution 제2종 분포
type Ⅱ error 제2종 오류
u-shaped distribution U형 분포
u-statistic U 통계량
ultimate cluster 최종군집
ultimate sampling unit 최종표집단위
umbrella alternative 우산형대립가설[대안]
unadjusted moment 비수정적률
unbalanced data 불균형자료
unbiased 비편향, 불편
unbiased confidence interval 비편향신뢰구간
unbiased error 비편향오차
unbiased estimate 비편향추정값
unbiased estimator 비편향추정량
unbiased most powerful test 비편향최강력검정[검증]
unbiased test 비편향검정[검증]
unbiased variance 비편향분산
unbiasedness 비편향성
uncertainty 불확실성
uncertainty principle 불확실성원리
uncorrelated 무상관
uncountability 비가산성, 셀 수 없음
uncountable 비가산, 셀 수 없는
uncountable set 비가산집합, 셀 수 없는 집
undercoverage 과소포함
under-dispersion 과소산포
under-fitting 과소적합
under-identified 과소식별
under-specification 과소특정화, 과소표기
unemployed person 실업자
unidentifiable 식별불가능
uniform continuity 고른 연속(성), 균등연속(성)
uniform convergence 고른 수렴, 균등수렴(성)
uniform distribution 균등분포, 균일분포
uniform intergrability 고른 적분가능성, 균등적분가능성
unform random variable 균등확률변수, 균일확률변수
uniform sampling fraction 균등표집[표본추출]비
uniform spectrum 균등 스펙트럼
uniformity trial 균일도시험
uniformly better decision function 균일하게 보다 나은 결정함수
uniformly continuous 고른 연속, 균등연속
uniformly minimum risk 균일 최소위험
uniformly minimum variance unbiased 균일최소분산비편향추정량
estimator
uniformly most efficient 균일최고효율
uniformly most powerful test 균일최강력검정[검증]
unimodal 단봉의
unimodal distribution 단봉분포, 일봉분포
union 합집합
union-intersection principle 합교원리
union of sets 집합의 합
unique factor 유일인자
unit 단위
unit distance 단위거리
unit distribution 단위분포
unit length 단위길이
unit matrix 단위행렬
unit normal variate 단위정규변량
unit number 단위수
unit of analysis 분석단위
unit vector 단위백터
univariate distribution 일변량분포, 단위변량분포
universe 모집단, 전체집단
unordered pair 무순서짝, 순서없는 짝
up-and-down method 상하법
up-cross 상향교차
updating 최신화
upper bound 상계
upper control limit 관리상한
upper limit 상단, 위끝, 위한계, 상한
upper quality level 상한품질수준
upper set 상위집합
upward rank 상향순위
upward trend 상향추세
urn model 항아리모형
utility 효용
vague distribution 모호분포
validation procedure 타당성검사절차
validity 타당성, 타당도
value 값
value added 부가가치
value index 가치지수
value of function 함수값
vanity effect 허영효과
variability 변이(성), 변동
variable 변수, 변량
variable sample size 가변표본크기
variable sampling rate 가변추출[표집]비
variance 분산
variance component model 분산성분모형
variance-covariance matrix 분산공분산행렬
variance decomposition 분산분해
variance function 분산함수
variance inflation factor 분산팽창[확대]인수[인자]
variance matrix 분산행렬
variance ratio 분산비
variance stabilization 분산안정화
variate 변량, 변수
variate difference method 변량차분법
variate transformation 변량변환
variation flow analysis 변동유량분석
varimx rotation 배리맥스[분산최대]회전
variogram 변동도
vector 벡터
vector autoregressive model 벡터자기회귀모형
vector autoregressive moving avearage model 벡터자기회귀이동평균모형
vector moving-average model 벡터이동평균모형
vector space 벡터공간
vector-valued function 벡터값함수
Venn diagram 벤 도표
vertical axis 수직축
vital statistics 인구동태통계
Von-Mises distribution 폰-미제스 분포
wage 임금
wage rate 임금율
wage survey 임금조사
waiting line 대기선
waiting queue 대기행렬
waiting time 대기시간
waiting time distribution 대기시간분포
Wald distribution 왈드 분포
Wald statistic 왈드 통계량
Wald test 왈드 검정[검증]
Walsh average 왈쉬 평균
wavelet 잔물결, 소파동
weak 약한
weak convergence 약수렴
weak law of large numbers 대수의 약법칙, 큰 수의 약법칙
weakly stationary process 약정상과정, 광의의 정상과정
wearout failure 마모고장
wearout period 마모고장기간
wearout replacement 마모교환
Weibull distribution 와이블분포
weighing design 칭량설계
weight 가중값, 가중치
weight function 가중값함수, 가중치함수
weighted arithmetic mean 가중산술평균
weighted average 가중평균
weighted index number 가중지수
weighted least squares method 가중최소제곱법
weighted mean 가중평균
weighted moving average 가중이동평균
weighted regression 가중회귀
white noise 백색잡음, 순수잡음
Whittaker periodogram 휘타커 주기도
Whittle distribution 위틀 분포
whole event 전체사건
whole-plot error 주구오차
wholesale price index 도매물가지수
wide sense stationary process 광의의 정상과정
Wiener-Hopf technique 위너-호프 기법
Wiener integral 위너 적분
Wiener-Khintchin theorem 위너-킨친 정리
Wiener process 위너 과정
Wilcoxon rank sum test 윌콕슨 순위합검정[검증]
Wilcoxon signed rank test 윌콕슨 부호순위검정[검증]
window 윈도우, 창
Winsorized mean 윈저화 평균
Winsorized sum of squares 윈저화 제곱합
Wishart distribution 위샤트 분포
within class variation 계급내변동
Wold's decomposition theorem 월드의 분해정리
working mean 가평균
wrapped distribution 겹쳐진 분포
wrapped normal distribution 겹쳐진 정규분포
wrapped Poisson distribution 겹쳐진 포아송분포
Yates' correction 예이츠의 수정
Youden square 유덴 방격[정방]
Young-Householder transformation 영-하우스홀더 변환
Yule process 율 과정
Yule's coefficient of association 율의 연관성계수
Yule's hyperbolic distribution 율의 쌍곡선분포
Yule-Walker equation 율-워커 방정식
Z-score Z 점수
Z-transformation Z 변환
zero 영
zero correlation 영상관
zero defect 무결점
zero dimension 영차원
zero matrix 영행렬
zero-one law 영일(0-1)법칙
zero order correlation 영차의 상관
zero-sum game 영합 게임, 영의 합 게임
zeta distribution 제타분포
zig zag sampling 지그재그 표집, 갈짓자형 표집
Zipf's law 지프의 법칙
zonal polynomial 띠모양다항식, 대형다항식
 invalid-file
invalid-file invalid-file
invalid-file

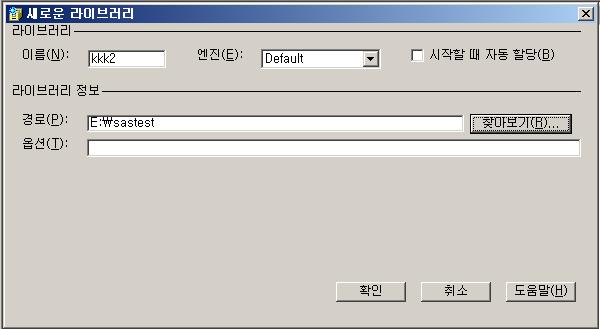
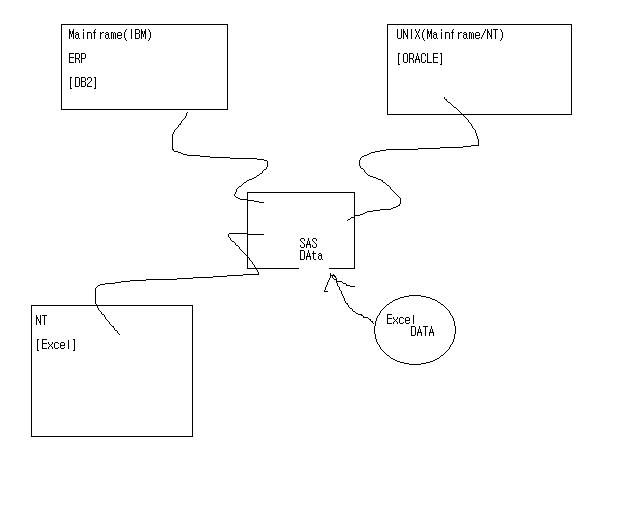
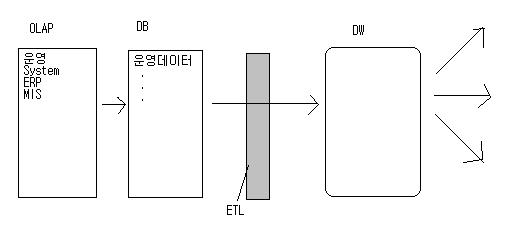
 invalid-file
invalid-file