검색결과 리스트
표준정규분포에 해당되는 글 1건
- 2007.02.21 표준정규분포와 t-분포 2
표준 정규 분포 자유도가 1인 t분포 빨간색이 표준정규분포, 파랑색이 t분포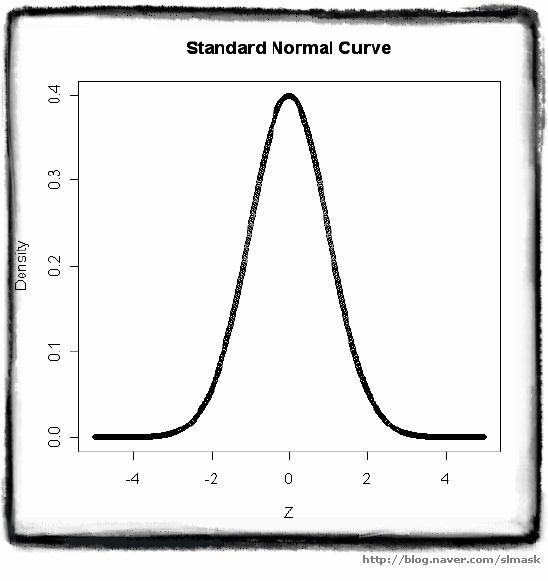
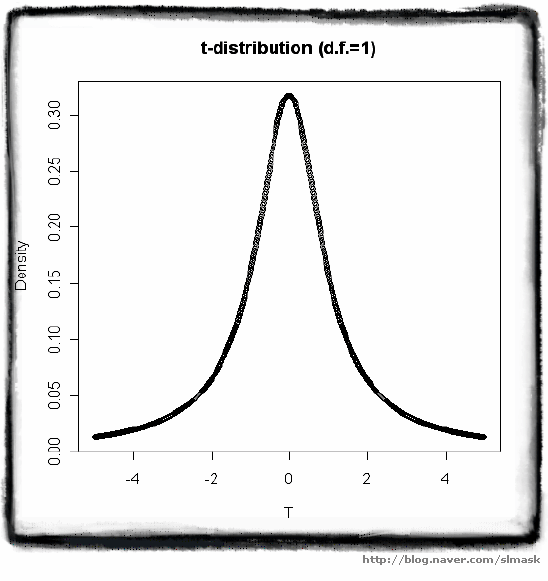
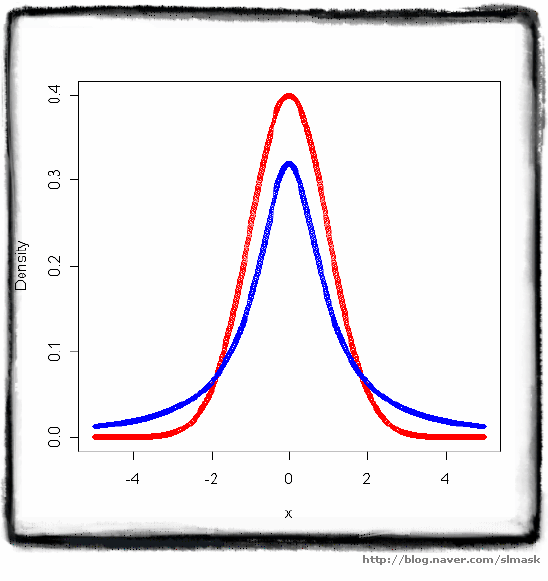
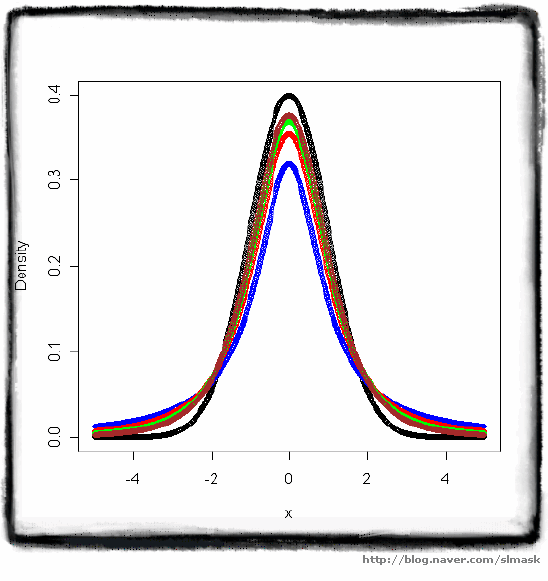
검정색 선 : 표준정규분포
파랑색 선 : t-분포 (df = 1)
빨강색 선 : t-분포 (df = 2)
초록색 선 : t-분포 (df = 3)
갈 색 선 : t-분포 (df = 4)
>>아래에서 보는 것처럼, t-분포의 자유도가 높을 수록 표준정규분포에 근사함을 알 수 있다.
표준정규분포 설명
내가 이 게시판에 올린 제목을 보고 당황한 사람이 있을거라 생각한다. 하지만 의심을 하지말고 일단 끝까지 읽어보길 바란다.
미안하지만 아직 표준정규분포를 모르는 사람들은 주변 사람들에게 수학의 정석을 빌려 찾아보길 바란다.
(아님 배울때까지 기다렸다가 이 글을 읽기 바란다.)
이놈을 처음 만난 날을 아직 잊을 수가 없다. 나는 수업도 안 듣고 이놈만 50분동안 째려 보았으니 말이다.
먼저 이 곡선을 뚫어져라 쳐다 보자. 특정 구간에서 곡선의 밑 면적은 해당 확률변수의 범위에 따른 확률을 나타낸다... 그리고 이 곡선에 있어서 x축은 점!근!선! 이다. 즉, 절대 만나지는 않는다는 것이다.
다시 말해서, 확률이 0일 수는 없다는 것이다. 하다 못해 내가 전교 500등을 해도 전교 1등을 할 확률이 절대 없지는 않다는 것이다. 이것이 첫번째 교훈.. Impossible Is Nothing (어디서 많이 본 듯 하다는.....*ㅡㅡ*쿨럭)
그리고 또한번 째려 보자. 과연 이 곡선에서 상위 0.1%의 밑면적과 평균에서 전후 0.1%의 밑면적은 얼마나 차이가 날까..
여기서 두번째 교훈... 남들 "만큼" 해서는 최고가 될 수 없다.
그리고 이번엔 이놈의 한가운데를 가로지르는 y축을 보자. x=0 즉, "평균"의 면적은... 직선이므로. 그 면적이 0다. 즉 이세상에 평균이란 없는 것이다... 이 무슨 궤변인고 하니..
세상은 y축이라는 기준을 따라 (+) 아니면 (-)다. 발전하거나, 뒤쳐지거나.. 정체란 있을수 없다
설령 아무리 공부를 열심히 해도 성적이 오르지 않는다 해도.. 그것은 정체가 아니라 발전이다. 그렇지 않으면 점차 퇴보할 뿐이다. 인생은 너무나 가파른 산이어서, 오르다 쉬는 순간에는 그만큼 미끄러져 내려가고 있는 것이다.
그리고 이번엔 이 곡선의 오른쪽 끝을 찾아보자.. 찾았는가?---->Yes 한 사람은 거짓말쟁이다. 아까도 말했듯 x축은 점근선이다. 즉, 곡선은 점점 x축에 가까워지면서 끝없이 나아가고 있다.
여기서 네번째, 나는 절대로 최고가 아니다! 세상엔 나보다 우월한 존재가 항상 존재한다. 따라서 나는 멈추어서는 안된다. 계속 나아가야만 한다! 는 것이다.
오늘 나의 헛소리는 여기까지!!! 일어주셔서 감사합니다~~~~~